Калькулятор объёма конуса

Печь на отработанном масле: варианты изготовления устройства своими руками

Основные сведения о хвостовиках и их обозначение

Существует несколько видов исполнения инструментального конуса. Он может содержать резьбу, лапку или обходиться без них.

В его торце может быть нарезана резьба, которую делают для закрепления инструмента на шпинделе с использованием штревеля. Это специальный шток, предотвращающий выпадение инструмента. Также с его помощью изделие можно извлечь, если его случайным образом заклинит в шпинделе.

Если хвостовик изготовлен с лапкой, то она удерживает инструмент в шпинделе за счет того, что закреплена в специальном пазу. Лапка имеет два предназначения, с ее помощью легче достать изделие из шпинделя, а также создается жесткая фиксация и не будет проворачивания.

Также можно встретить исполнение с несколькими канавками и отверстиями. Они имеют разную глубину и размеры. Их задача – подводить к режущему инструменту смазочно-охлаждающую жидкость.

Хвостовики инструмента бывают различной конструкции и обозначаются буквенным кодом. Ниже приведена их расшифровка:

• BI – внутренний, имеется паз;
• ВЕ – наружный, имеется лапка;
• AI – внутренний, имеется отверстие по оси;
• АЕ – наружный, имеется отверстие по оси с резьбой;
• BIK – внутренний, имеются паз и отверстие для подачи смазочно-охлаждающей жидкости (СОЖ);
• ВЕК – наружный, имеется лапка и отверстие для подачи СОЖ;
• AIK – внутренний, содержит отверстия по оси и для подачи СОЖ;
• АЕК – наружный, содержит отверстие по оси с резьбой и отверстие для подачи СОЖ.

Наружный и внутренний соответствуют своим названиям. В зависимости от используемого инструмента, следует выбирать исполнение наружное или внутреннее.

Обобщения и замечания[править]

• Используя вышеприведённую технику, можно построить развёртку практически любого объекта со сложной топографией.
• При этом следует иметь в виду, что при работе с металлом следует брать внутренние размеры детали, т.к. при гибке и/или закатке, внешняя поверхность металла тянется, а внутренняя остаётся неизменной. (Верно при использовании современного гибочного оборудования. На устаревшем оборудовании, следует вводить поправки на износ поверхностей, и точность работы станка.)
• При работе с металлом, толщиной свыше 6 мм, в зависимости от типа, марки металла и используемого гибочного оборудования — размеры следует брать не по внутренней стороне, а по «средней линии», которая проходит на половине толщины металла. Либо считать места сгибов не как прямые углы, а как дуги.
• При изготовлении из металла, линии разметки (прямые, а не вспомогательные диагонали) могут использоваться как линии гиба, с последующей доводкой контура молотком/киянкой на вспомогательной поверхности.

Особенности построения уклона и конусности

Область черчения развивалась на протяжении достаточно длительного периода. Она уже много столетий назад применялась для передачи накопленных знаний и навыков. Сегодня изготовление всех изделия может проводится исключительно при применении чертежей. При этом ему больше всего внимания уделяется при наладке массового производства. За длительный период развития черчения были разработаны стандарты, которые позволяют существенно повысить степень читаемости всей информации. Примером можно назвать ГОСТ 8593-81. Он во многом характеризует конусность и уклон, применяемые методы для их отображения. Начертательная геометрия применяется для изучения современной науки, а также создания различной техники. Кроме этого, были разработаны самые различные таблицы соответствия, которые могут применяться при проведении непосредственных расчетов.

Различные понятия, к примеру, сопряжение, уклон и конусность отображаются определенным образом. При этом учитывается область применения разрабатываемой технической документации и многие другие моменты.

К особенностям построения угла и конусности можно отнести следующие моменты:

1. Основные линии отображаются более жирным начертанием, за исключением случая, когда на поверхности находится резьба.
2. При проведении работы могут применяться самые различные инструменты. Все зависит от того, какой метод построения применяется в конкретном случае. Примером можно назвать прямоугольный треугольник, при помощи которого выдерживается прямой угол или транспортир.
3. Отображение основных размеров проводится в зависимости от особенностей чертежа. Чаще всего указывается базовая величина, с помощью которой определяются другие. На сегодняшний день метод прямого определения размеров, когда приходится с учетом масштаба измерять линии и углы при помощи соответствующих инструментов практически не применяется. Это связано с трудностями, которые возникают на производственной линии.

В целом можно сказать, что основные стандарты учитываются специалистом при непосредственном проведении работы по построению чертежа.

В проектной документации, в которой зачастую отображается конусность, при необходимости дополнительная информация выводится в отдельную таблицу.

Для чего используется конус

Мы подробно разобрали самые простые варианты как сделать правильный конус из бумаги. Для чего используется эта поделка? Направления у нее самые различные:

• геометрических выставок;
• объемных поделок;
• изготовления маскарадных шляп.

Ваша фантазия подскажет вам, где еще может применяться конус. А мы поможем вам вдохновиться с помощью простой конусной поделки елочки.

Ёлка из конуса

Для нее потребуется:

• картон;
• бумага для подарков;
• скотч;
• декоративные предметы;
• ножницы.

В основе изделия, как вы уже поняли, лежит конус. Изготовьте его по одной из предложенных выше инструкций.

Далее работаем по схеме:

1. Полученный конус, оборачиваем бумагой для подарков. Крепим кончик материала к верхушке скотчем и аккуратно оборачиваем бумагу по фигуре. Отрезаем лишний материал.
2. Крепим концы с помощью скотча.
3. Вы не поверите, но елочка готова. Осталось ее украсить как настоящую. С этой целью могут подойти пуговицы, большие бусины и миниатюрные новогодние игрушки.

В ёлке можно сделать отверстия. И если она достаточно широка, поместите внутрь конуса новогодние огоньки. В темноте, они будут приятно мелькать, создавая приятную атмосферу.

http://ngeometry.ru/postroenie-razvertki-konusa.htmlhttp://stroyday.ru/kalkulyatory/obshhestroitelnye-voprosy/kalkulyatory-rascheta-razmerov-razvertki-konusa.htmlhttp://megamaster.info/kak-sdelat-konus-iz-bumagi/

Опасности токсических веществ

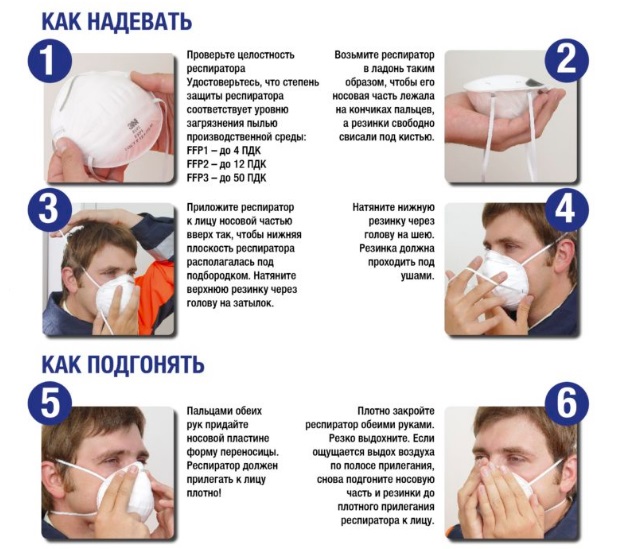
Важно знать, что многие химические соединения, пары краски, попадая через органы дыхания в человеческий организм, приводят к состоянию гипоксии. Первым делом страдает центральная нервная система, появляются такие симптомы:

•  нарушается координация движений, сложно ориентироваться в пространстве;
•  возникает боязнь яркого и приглушенного света;
•  теряется обоняние и вкус;
•  появляются разнообразные галлюцинации;
•  возникают панические атаки.

Отравление токсическими веществами вызывает следующие соматические реакции:

•  головокружение;
•  носовое кровотечение;
•  боли в суставах;
•  рвота, которая не связана с испорченными продуктами питания;
•  тахикардия (учащенное биение сердца).

Чтобы не возникали приведенные выше симптомы, важно использовать подходящий респиратор во время нанесения краски или в ходе работы с химическими веществами. При возникновении одного из перечисленных симптомов, незамедлительно нужно выйти на улицу и обратиться за врачебной помощью

В некоторых случаях наблюдаются хронические отравления из-за того, что человек систематически работает с вредной химической продукцией без использования респиратора или неправильно его применяет.

Это интересно: Пистолет пистолету рознь — чем наносить герметик

Круглый конус в геометрии

Приведем геометрическое определение этой фигуры. Круглым конусом называется поверхность, которая образована прямыми отрезками, соединяющими все точки некоторой окружности с одной-единственной точкой пространства. Эта единственная точка не должна принадлежать плоскости, в которой лежит окружность. Если вместо окружности взять круг, то указанный способ также приводит к получению конуса.

Круг называется основанием фигуры, его окружность — это директриса. Отрезки, соединяющие точку с директрисой, называются генератрисами или образующими, а точка, где они пересекаются — это вершина конуса.

Круглый конус может быть прямым и наклонным. Обе фигуры показаны ниже на рисунке.

Разница между ними заключается в следующем: если перпендикуляр из вершины конуса падает точно в центр окружности, то конус будет прямым. Для него перпендикуляр, который называется высотой фигуры, является частью его оси. В случае конуса наклонного высота и ось образуют некоторый острый угол.

Ввиду простоты и симметричности фигуры далее будем рассматривать свойства только прямого конуса с круглым основанием.

Тычковые ножи для самообороны

Калькуляторы расчета размеров развертки конуса — с пояснениями

Иногда в ходе выполнения тех или иных хозяйственных работ мастер встаёт перед проблемой изготовления конуса – полного или усеченного. Это могут быть операции, скажем, с тонким листовым металлом, эластичным пластиком, обычной тканью или даже бумагой или картоном. А задачи встречаются самый разные – изготовление кожухов, переходников с одного диаметра на другой, козырьков или дефлекторов для дымохода или вентиляции, воронок для водостоков, самодельного абажура. А может быть даже просто маскарадного костюма для ребенка или поделок, заданных учителем труда на дом.

Калькуляторы расчета размеров развертки конуса

Чтобы из плоского материала свернуть объёмную фигуру с заданными параметрами, необходимо вычертить развертку. А для этого требуется рассчитать математически и перенести графически необходимые точные размеры этой плоской фигуры. Как это делается – рассмотрим в настоящей публикации. Помогут нам в этом вопросе калькуляторы расчета размеров развертки конуса.

Несколько слов о рассчитываемых параметрах

Понять принцип расчета будет несложно, разобравшись со следующей схемой:

Усеченный конус с определяющими размерами и его развёртка. Показан усеченный конус, но с полным — принцип не меняется, а расчеты и построение становятся даже проще.

Итак, сам конус определяется радиусами оснований (нижней и верхней окружности) R1 и R2, и высотой Н. Понятно, что если конус не усеченный, то R2 просто равно нулю.

Буквой L обозначена длина боковой стороны (образующей) конуса. Она в некоторых случаях уже известна – например, требуется сделать конус по образцу или выкроить материал для обтяжки уже имеющегося каркаса. Но если она неизвестна – не беда, ее несложно рассчитать.

Справа показана развёртка. Она для усеченного конуса ограничена сектором кольца, образованного двумя дугами, внешней и внутренней, с радиусами Rb и Rs. Для полного конуса Rs также будет равен нулю. Хорошо видно, что Rb = Rs + L

Угловую длину сектора определяет центральный угол f, который в любом случае предстоит рассчитать.

Все расчеты займут буквально минуту, если воспользоваться предлагаемыми калькуляторами:

(Если она уже известна – шаг пропускается)

Перейти к расчётам

Шаг 3 – определение величины центрального угла f

Перейти к расчётам

* * * * * * *

Итак, все данные имеются. Остается на листе бумаги циркулем провести две дуги рассчитанных радиусов. А затем из точки центра с помощью транспортира прочертить два луча под рассчитанным углом – они ограничат развертку по угловой длине.

Существуют и чисто геометрические методы построения довольно точной развертки конуса, без проведения расчётов. Один из них подробно описан в статье нашего портала «Как сделать абажур своими руками».

stroyday.ru

С понижением линии обуха

Интересно почитать

Акция Альфабанка

Развертка наклонного конуса

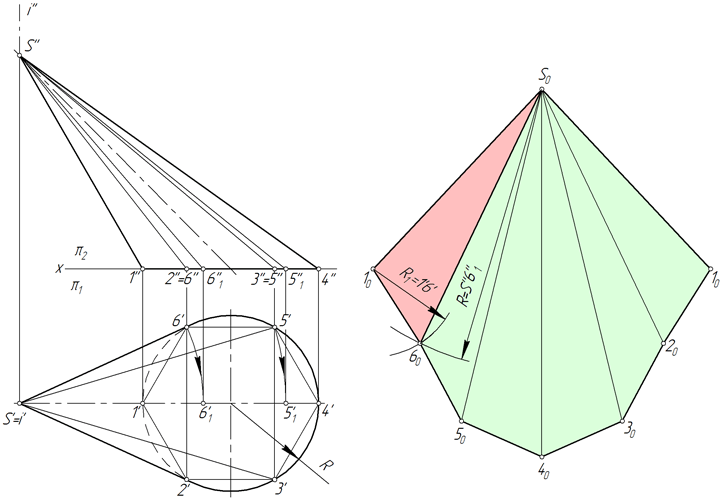
Рассмотрим порядок построения развертки боковой поверхности наклонного конуса методом аппроксимации (приближения).

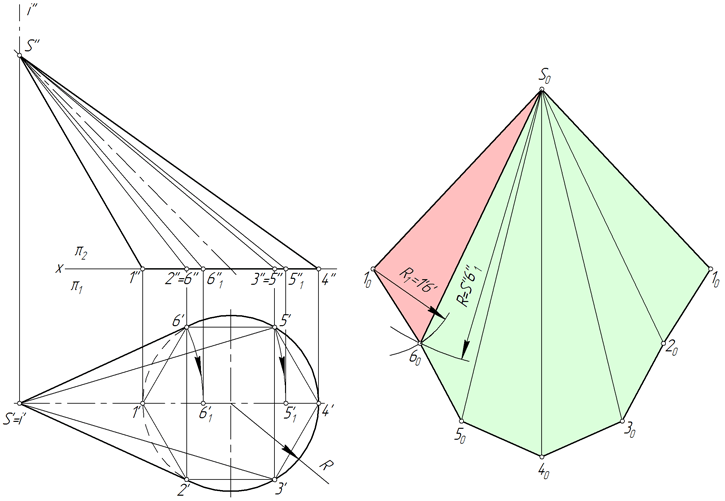
1. Вписываем в окружность основания конуса шестиугольник 123456. Соединяем точки 1, 2, 3, 4, 5 и 6 с вершиной S. Пирамида S123456, построенная таким образом, с некоторой степенью приближения является заменой конической поверхности и используется в этом качестве в дальнейших построениях.
2. Определяем натуральные величины ребер пирамиды, используя способ вращения вокруг проецирующей прямой: в примере используется ось i, перпендикулярная горизонтальной плоскости проекций и проходящая через вершину S. Так, в результате вращения ребра S5 его новая горизонтальная проекция S’5’1 занимает положение, при котором она параллельна фронтальной плоскости π2. Соответственно, S’’5’’1 – натуральная величина S5.
3. Строим развертку боковой поверхности пирамиды S123456, состоящую из шести треугольников: S16, S65, S54, S43, S32, S21. Построение каждого треугольника выполняется по трем сторонам. Например, у △S16 длина S1=S’’1’’, S6=S’’6’’1, 16=1’6’.

Степень соответствия приближенной развертки действительной зависит от количества граней вписанной пирамиды. Число граней выбирают, исходя из удобства чтения чертежа, требований к его точности, наличия характерных точек и линий, которые нужно перенести на развертку.

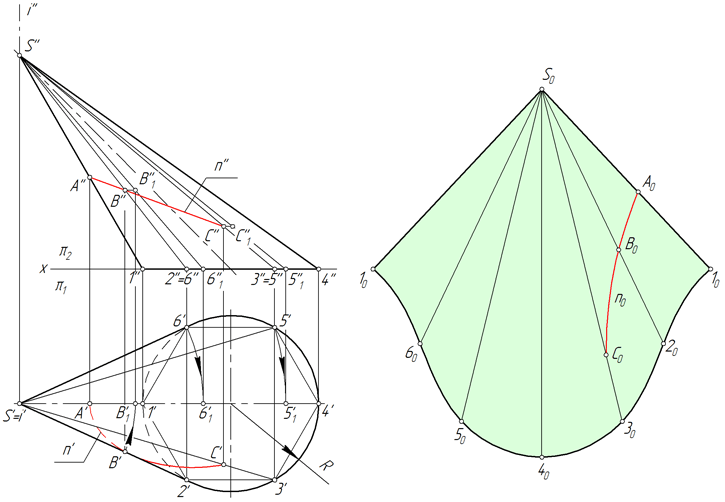
Перенос линии с поверхности конуса на развертку

Линия n, лежащая на поверхности конуса, образована в результате его пересечения с некоторой плоскостью (рисунок ниже). Рассмотрим алгоритм построения линии n на развертке.

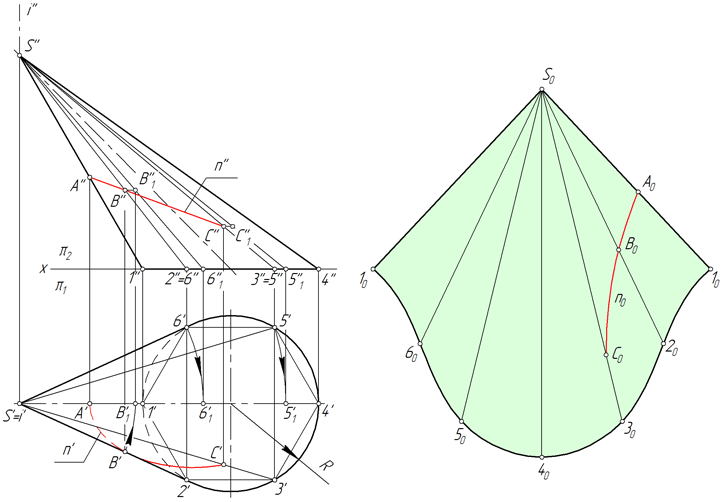
1. Находим проекции точек A, B и C, в которых линия n пересекает ребра вписанной в конус пирамиды S123456.
2. Определяем натуральную величину отрезков SA, SB, SC способом вращения вокруг проецирующей прямой. В рассматриваемом примере SA=S’’A’’, SB=S’’B’’1, SC=S’’C’’1.
3. Находим положение точек A, B, C на соответствующих им ребрах пирамиды, откладывая на развертке отрезки SA=S’’A’’, SB=S’’B’’1, SC=S’’C’’1.
4. Соединяем точки A, B, C плавной линией.

Как устроена стиральная машина

Развертка усеченного конуса

Описываемый ниже способ построения развертки прямого кругового усеченного конуса основан на принципе подобия.

Алгоритм

1. Строим вспомогательный конус ε, подобный конусу ω, как это показано на рисунке выше. Для удобства построения величину диаметра d выбираем таким образом, чтобы соотношение t=D/d выражалось целым числом. В рассматриваемом примере t=2.
2. Строим развертку боковой поверхности конуса ε – S0A01020304050A0 и на биссектрисе угла A0S0A0 отмечаем точку O0, выбрав ее расположение произвольно.
3. Проводим прямые O0A0, O010, O020, O030, O040, O050, O0A0 и на них откладываем отрезки =t×|O0A0|, = t×|O010|, =t×|O020|, =t×|O030|, =t×|O040|, =t×|O050|, =t×|O0A0| соответственно, где t=D/d. Соединяем точки A10, 110, 210, 310, 410, 510, A10 плавной линией.
4. Из точек A10, 110, 210, 310, 410, 510, A10 проводим лучи, которые параллельны соответственно прямым A0S0, 10S0, 20S0, 30S0, 40S0, 50S0, A0S0, и на них откладываем отрезки A10B10, 110120, 210220, 310320, 410420, 510520, A10B10, равные l – образующей усеченного конуса. Проводим линию B10120220320420520B10.

Развертка наклонного конуса

Рассмотрим порядок построения развертки боковой поверхности наклонного конуса методом аппроксимации (приближения).

Алгоритм

1. Вписываем в окружность основания конуса шестиугольник 123456. Соединяем точки 1, 2, 3, 4, 5 и 6 с вершиной S. Пирамида S123456, построенная таким образом, с некоторой степенью приближения является заменой конической поверхности и используется в этом качестве в дальнейших построениях.
2. Определяем натуральные величины ребер пирамиды, используя вокруг проецирующей прямой: в примере используется ось i, перпендикулярная горизонтальной плоскости проекций и проходящая через вершину S.
   Так, в результате вращения ребра S5 его новая горизонтальная проекция S’5’₁ занимает положение, при котором она параллельна фронтальной плоскости π₂. Соответственно, S’’5’’₁ – натуральная величина S5.
3. Строим развертку боковой поверхности пирамиды S123456, состоящую из шести треугольников: S16, S65, S54, S43, S32, S21. Построение каждого треугольника выполняется по трем сторонам. Например, у △S16 длина S1=S’’1’’, S6=S’’6’’₁, 16=1’6’.

Степень соответствия приближенной развертки действительной зависит от количества граней вписанной пирамиды. Число граней выбирают, исходя из удобства чтения чертежа, требований к его точности, наличия характерных точек и линий, которые нужно перенести на развертку.

Перенос линии с поверхности конуса на развертку

Линия n, лежащая на поверхности конуса, образована в результате его пересечения с некоторой плоскостью (рисунок ниже). Рассмотрим алгоритм построения линии n на развертке.

Алгоритм

1. Находим проекции точек A, B и C, в которых линия n пересекает ребра вписанной в конус пирамиды S123456.
2. Определяем натуральную величину отрезков SA, SB, SC способом вращения вокруг проецирующей прямой. В рассматриваемом примере SA=S’’A’’, SB=S’’B’’₁, SC=S’’C’’₁.
3. Находим положение точек A, B, C на соответствующих им ребрах пирамиды, откладывая на развертке отрезки SA=S’’A’’, SB=S’’B’’₁, SC=S’’C’’₁.
4. Соединяем точки A, B, Cплавной линией.

Уклоны и конусность — Техническое черчение

• Уклоном прямой ВС относительно прямой AB (фиг. 57, а) называется отношение:
• i=AC/AB=tga
• Конусностью называется отношение разности диаметров двух попе­речных сечений конуса к расстоянию между ними (фиг. 57,б)
• k=(D-d)/l=2tga
• Таким образом,
• k = 2i
• Уклон и конусность могут быть указаны: а) в градусах; б) дробью простой, в виде отношения двух чисел или десятичной; в) в процентах.
• Например: конусность, выраженная в градусах — 11°25’16″; отношением —  1:5; дробью —0,2; в процентах — 20%, и соответственно этому уклон в градусах — 5°42’38″; отношением — 1:10; дробью—0,1; в процентах —  10%.
• Для конусов, применяемых в машиностроении, OCT/BKC 7652 устанавливает следующий ряд нормальных конусностей — 1 :3; 1 :5; 1 :8; 1 : 10; 1 :15; 1:20; 1 :30; 1:50; 1 :100; 1:200, а также 30, 45, 60, 75, 90 и 120°.
• Допускаются в особых случаях также конусности 1:1,5; 1:7; 1:12 и 110°.

Если требуется через точку Л, лежащую на прямой AB (фиг. 57, в), провести прямую с уклоном i=l:n относительно AB, надо отложить от точки А по направлению данной прямой n произвольных единиц; в конце полученного отрезка AB восстановить перпендикуляр ЕС длиной в одну такую же единицу. Гипотенуза AС построенного прямоугольного треугольника определяет искомую прямую.

1. Для проведения прямой заданного уклона l:n через точку M, не лежащую на данной прямой AB, можно поступать двояко (фиг. 58):
2. 1)    построить в стороне прямоугольный треугольник KLN (или KLN1) с отношением катетов l:n, причём катет KL ll AB; затем через точку M провести искомую прямую MD (или MD1) параллельно гипотенузе вспомогательного треугольника KN (или LN1);

2)    опустить из точки M перпендикуляр ME на прямую AВ и при­нять его за единицу. По направлению прямой AB влево или вправо от точки E отложить n таких же отрезков; гипотенузы DM или MD1 по­строенных таким образом прямоугольных треугольников являются иско­мыми прямыми.

Построение конусности l:n относительно данной оси сводится к построению уклонов l:n/2 с каждой стороны оси.

Уклон или конусность чаще всего указывается в процентах или отношением единицы к целому числу. Рассмотрим эти способы построе­ния на примерах.

Пример 1. Требуется построить профиль сечения швеллера № 5 ОСТ 10017-39 (фиг. 59, а), если известно, что уклон его полок равен 10%

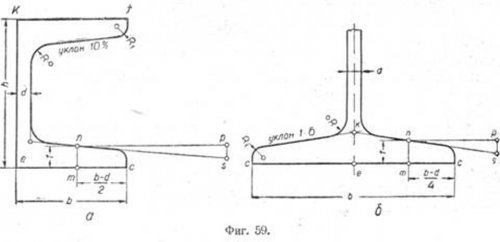
Размеры для построения берём из ОСТ 10017-39.

Проводим вертикальную прямую ek, равную h = 50 мм. Из точек e и k проводим прямые ec и kf, равные ширине полки b = 37 мм.

Ввиду того, что обе полки швеллера одинаковы, ограничимся построе­нием только одной из них. Откладываем на прямой ec от точки с отре­зок cm, равный (b-d)/2.

В точке m на перпендикуляре к прямой ec от­кладываем отрезок mn, равный t = 7 мм. Через точку n проводим прямую np параллельно ec, равную 50 мм.

• Перпендикулярно к np из точки p проводим отрезок ps, равный по длине десяти процентам отрезка np. Величина его определяется из от­ношения:
• ps/np=10/100,
• откуда
• ps=10*50/100=5 мм.

Прямая sn является искомой прямой, имеющей уклон 10% по отно­шению к ec. Дальнейшее построение профиля не представляет затруд­нений.

Отрезок np можно взять любой длины. Чем больше его величина, тем точнее будет построена прямая уклона. Однако для удобства вы­числения следует принимать отрезок np таким, чтобы длина его, выра­жаемая в миллиметрах, оканчивалась на 0 или 5.

П p и м e p 2. Построить профиль сечения двутавра № 10 ОСТ 10016-39 (фиг. 59, б), если известно, что уклон полок его равен 1:6. Размеры для построения берём из ОСТ 10016-39.

Проводим горизонтальную прямую cc, равную ширине полки b = = 68 мм. Через точку e, являющуюся серединой ширины полки, прово­дим вертикальную линию. Откладываем от точки с отрезок mс, равный

(b-d)/4. В точке m, перпендикулярно к отрезку cc, проводим прямую и

на ней откладываем отрезок mn, равный t=6,5 мм. Через точку n проводим горизонтальную прямую np, равную 30 мм, которая будет служить катетом прямоугольного треугольника. Чем длиннее катет, тем точнее будет построен уклон. Для удобства принимают длину отрезка np кратной шести, тогда второй катет будет равен целому числу. Вели­чина второго катета определяется из формулы

1. i=ps/np=1/6
2. где i — заданный уклон.
3. Подставив в формулу числовые значения, получим
4. ps=30/6=5 мм.

Откладываем в точке p под углом 90° к прямой np вычисленную длину второго катета, получим точку 5. Проводим через точки s и n прямую, которая и будет соответствовать искомой прямой, имеющей уклон 1 :6.

Построение сопряжений такое же, как и для швеллера в предыду­щем примере.

Инструкция изготовления простого конуса

Сделать конус в основе которого лежит бумага очень просто. На всю работу уходит до пяти минут. Достаточно перед работой изготовить верный чертеж и свернуть материал правильным образом.

Простой конус схема

Для первой работы потребуется:

• лист А4;
• циркуль с вставленным карандашом;
• длинная линейка
• ножницы;
• степлер или клей.

Как сделать конус из бумаги пошагово:

1. Берем бумагу. Определяем центр листа. Отмечаем место.
2. В отмеченную точку ставим острие циркуля и чертим круг. Вырезаем нарисованную фигуру. На полученной заготовке от края к уже установленному центру проводим линию. Делаем по этой линии разрез.
3. Из сделанного круга с разрезом, сворачиваем воронку. Скрепляем края фигуры с помощью степлера или клея.

Конус готов. Готовую фигуру можно использовать для разнообразных поделок. А если добавить к нашей фигуре шар, то получится поделка для выставки на геометрическую тематику.

Развертка усеченного конуса

Как мы видели, рассматриваемая фигура образована тремя поверхностями. Две из них представляют основания, а третья является боковой. Сумма площадей этих поверхностей является полной поверхностью усеченного конуса. В трехмерном пространстве ее площадь вычислять неудобно, поскольку сама величина является двумерной. В связи с этим при возникновении проблемы определения площади поверхности пространственных фигур, их принято представлять на плоскости.

В нашем случае развертку получить достаточно просто. Для этого следует мысленно отрезать по соответствующим окружностям основания от фигуры. Затем, необходимо разрезать вдоль образующей и раскрыть поверхность боковую. В итоге получится результат, показанный на фото.

Она представляет собой два разных круга и часть кругового сектора, у которого вырезан центр.

Основные виды кухонных ножей

Как сделать конус из картона

Вы узнали, как сделать конус из простой бумаги А4, но, если вам нужна плотная поделка, лучше воспользоваться картоном. Материалы и инструменты остаются теми же, что и в предыдущих поделках. Различие заключается только в оттенке картона, его подбираем исходя из предназначения.

Будущий конус будет достаточно прочным за счет чего, его применение может быть широким. Подобную методику работы мы уже рассмотрели выше, но это изготовление все же отличается.

1. Возьмите картон нужного оттенка. Определите середину листа и используя циркуль начертите круг.
2. Полученную окружность нужно разделить на четыре равные доли. Для разделения фигуры на правильные части проведите через полученную ранее точку в центре прямые линии.
3. Складываем круг в разных направлениях. Вы получите четыре сегмента. Один из них нужно вырезать.
4. Полученную заготовку сворачиваем образуя колпак. Так как картон может не сразу склеиться, закрепляем низ фигуры степлером. И только затем промазываем фигуру ПВА.

Плотный конус готов. Если вам нужна не одна геометрическая фигура, а несколько, первый полученный круг, в котором уже вырезана одна четверть, можно использовать в качестве шаблона.

Ограждение для 6 мусорных контейнеров ТБО с устройством бетонной площадки и секцией КГО (Арт 31116)

Уклон

Плоские поверхности деталей, расположенные наклонно, обозначают на чертеже величиной уклона. Как подсчитать эту величину, покажем на примере. Клин, изображенный на рис. 6.40, я, имеет наклонную поверхность, уклон которой нужно определить. Из размера наибольшей высоты клина вычтем размер наименьшей высоты: 50 – 40 = 10 мм. Разность между этими величинами можно рассматривать как размер катета прямоугольного треугольника, образовавшегося после проведения на чертеже горизонтальной линии (рис. 6.40, б). Величиной уклона будет отношение размера меньшего катета к размеру горизонтальной линии. В данном случае нужно разделить 10 на 100. Величина уклона клина будет 1:10.

Рис. 6.40. Определение величины уклона

На чертеже уклоны указывают знаком и отношением двух чисел, например 1:50; 3:5.

Если требуется изобразить на чертеже поверхность определенного уклона, например 3:20, вычерчивают прямоугольный треугольник, у которого один из катетов составляет три единицы длины, а второй – 20 таких же единиц (рис. 6.41).

Рис. 6.41. Построение уклонов и нанесение их величин

При вычерчивании деталей или при их разметке для построения линии по заданному уклону приходится проводить вспомогательные линии. Например, чтобы провести линию, уклон которой 1:4, через концевую точку вертикальной линии (рис. 6.42), отрезок прямой линии длиной 10 мм следует принять за единицу длины и отложить на продолжении горизонтальной линии четыре такие единицы (т.е. 40 мм). Затем через крайнее деление и верхнюю точку отрезка провести прямую линию.

Рис. 6.42. Построение линии по заданному уклону

Вершина знака уклона должна быть направлена в сторону наклона поверхности детали. Знак и размерное число располагают параллельно направлению, по отношению к которому задан уклон.

Что ещё можно сделать из бумажного конуса?

Бумажную заготовку для конуса можно использовать, чтобы сделать упаковку для сладкого подарка. Для этого на края, с внутренней стороны, добавляют кусочки двустороннего скотча, или же просто промазывают клеем.

Затем на эти участки помещаются листы гофрированной бумаги.

• Чтобы она красиво легла, нужно делать небольшие складки.
• После этого заготовка с бумагой склеивается в конус.
• Внутрь поделки помещаются конфеты или другие предметы, а гофрированный лист сверху завязывается ленточкой, образуя мешочек.
• На готовую упаковку можно добавить и другие декоративные элементы.

Бумажный конус можно использовать и для других поделок. Например, если делать его из плотного картона, то затем, с помощью ткани, получится создать вот такие игрушки животных или елочное украшение.

Какие тарифы лучше всего для ИП

Сообщить об опечатке