Как найти площадь любого треугольника

Особенности измерения квадратных метров квартиры

Осуществляя измерения квадратных метров комнаты необходимо учитывать следующие рекомендации: Измерять ширину стен лучше всего по линии потолка или пола, так значения будут более правдивыми; Не стоит полагаться на приблизительные расчеты или установленные ранее величины; Для того чтобы вычислить сумму площадей всей комнаты нужно сложить площади всей комнаты, которые вычисляются для каждой стены;

Выполняя вычисления площади, обязательно стоит вычитать излишки. Для тех, кто не знает, как посчитать, сколько метров стена сейчас создано множество программ, которые можно скачать для этих целей из интернета.

Как показывает практика, ничего сверхъестественного в подобных расчетах нет. Сделать их можно самостоятельно не прибегая к помощи специалистов. Для того чтобы перевести длину и ширину в квадратные метры порой просто необходимо вспомнить школьную программу. Возьмите на заметку! В том случае если при измерении стен выявляется наличие впадин или выпуклостей, то необходимо к высоте и ширине накинуть несколько сантиметров.

Видео по теме: квадратные метры в помещении

Немного теории

Чтобы рассчитать площадь помещения, достаточно иметь минимальный набор инструментов и знаний на уровне 5-го класса. Под рукой должны быть рулетка, карандаш и лист бумаги. Для определения площади необходимо длину умножить на ширину.

Важно! Стоит понимать, что эта формула действует только для идеально квадратной или прямоугольной квартиры, для сложной конфигурации есть свои проблемы, как и для тех квартир, в стенах которых предполагаются ниши

Что такое 1 см² и 1 м²

По сути, любую фигуру можно измерить в миллиметрах, сантиметрах, метрах и т.д. Если это значение в «квадрате», т.е. мм2, см2, м2 и т.д., то это говорит о том, что площадь измеряется в количестве квадратов, каждая сторона из которых равна одноименному значению – 1 мм2, 1 см2, 1 м2 и т.д. В строительстве берется за основу 1 м2.

Формулы

Чтобы узнать, как вычислить площадь комнаты в м2, достаточно провести несложные арифметические вычисления. Для этого просто измерить ее длину и ширину, потом сложить получившееся значение и умножить на 2: к примеру возьмем размер 160 см на 100 см. Умножаем цифры 160 на 100 и получаем 16000 см в квадрате.

Можно поступить еще проще и просто все стороны помещения перемножить: потолок, пол, стены.

Перевод квадратных сантиметров в квадратные метры

Перед тем, как узнать сколько в комнате квадратных метров, очень важно разобраться в самих значениях, ведь когда идет расчет с сотнями сантиметров, их в любом случае необходимо переводить в метры. Делается это по следующей формуле, уже на известном примере: 160 см * 100 см – разница величин (в одном метре – 100 сантиметров), в итоге получается 16000 см2, которые нужно разделить на 10000 и получим = 1.60 м2

Такими цифрами намного проще оперировать и запоминать. Тем более, что «квадратуру» помещения всегда измеряют именно в метрах. Для перевода необходимо подставлять следующие формулы:

• 8000 см² / 10000 = 0,8 м²;
• 34000 см² / 10000 = 3,4 м²;
• 2400 см²/ 10000 = 0,24 м².

Все достаточно просто и не составит труда составить такие несложные арифметические вычисления, даже школьнику

Очень важно перед тем, как узнать квадратуру комнаты, провести максимально точные измерения, после чего приступить к расчетам

Советы и рекомендации

Необходимо помнить, что геометрические параметры зданий редко могут быть идеальными. Поэтому для определения точных величин замеры лучше производить в нескольких местах, а затем выводить среднее арифметическое. Например, рассчитывая площадь комнаты по стенам, длину лучше измерять по потолку, плинтусу и в середине вертикальной плоскости. Высоту — в углах и середине стены по отвесу.

Чтобы вычислить периметр при наличии множества выступов и ниш разных форм, необходимо проложить вдоль всех элементов шнур, затем измерить его рулеткой.

Подсчитав точные параметры, можно идти в магазин за строительными материалами. Лучше показать схемы с нанесенными размерами продавцу-консультанту. Специалист поможет рассчитать расход материалов с учетом нахлеста, подбора рисунка обоев или потерь при резке плитки.

Общие сведения

Изучение того, как и какой буквой обозначается общая площадь, необходимо начать с определения данного понятия в математике.

Под площадью понимается характеристика, имеющая числовое выражение. Ею описывается геометрическая фигура в двухмерном пространстве.

Объект, по отношению к которому возникает вопрос, как обозначить в письменном выражении площадь, может быть плоским или искривленным.Обозначение площади дает представление о размере и параметрах изучаемой площади.

В отдельных литературных источниках общая площадь встречается под названием квадратуры. Фигура, для которой возможно обозначить площадь, имеет наименование квадрируемой. Геометрические объекты, для которых значение площади в полученном решении оказалось одинаковым, встречаются под названием равновеликих.

Возможность определения площади и обозначения ее буквой появилась благодаря интегральному исчислению в математике. Общее представление о данном понятии было получено в результате формулирования теории меры множества. Постулаты, составляющие данную теорию, являются правдивыми для большинства объектов, изучаемых в геометрии.

Возможность практического измерения данной величины отмечается в результате использования планиметра и специальной палетки.

Площадь, обозначение которой становится доступным в результате ее числового выражения, характеризуется следующими параметрами:

1. Положительная. В числе ее характеристик отсутствует понятие отрицательного значения.
2. Аддитивная. Данный показатель относительно любого геометрического объекта определяется как суммированное значение объектов, образующих изучаемую фигуру при отсутствии внутренних ограничений.
3. Инвариантная. Позволяет приравнивать площади фигур, которые в движении переходят друг в друга и полностью совпадают.
4. Нормированная. Соответствует правилу, согласно которому 1 составляет площадь единичного квадрата.
5. Монотонная. Параметр площади отдельной части геометрического объекта не превышает общую площадь всей изучаемой фигуры.

Знак площади, используемый в математике, появился в результате присвоения данного параметра для многоугольных геометрических объектов. Впоследствии перечень фигур, в отношении к площади которых использовалось обозначение буквой, увеличился на группу квадрируемых объектов.

Обратите внимание, к категории квадрируемой относится объект, поддающийся вписыванию в пределы многоугольника. Также достоверной является способность заключить многоугольник в данный квадрируемый объект

Общее понимание категории позволяет ее трактовать в качестве числовой характеристики. При этом этот признак используется по отношению только к поверхности двухмерной, находящейся в пространстве трехмерном.

Для данного показателя присуща система измерения. Основными единицами, дающими представление о величине геометрического объекта, являются сантиметры, миллиметры, дециметры, метры, километры. В ряде источников встречается упоминание проведенных измерений в арах, гектарах. Отличительная особенность, свойственная для рассматриваемого показателя, возведение единиц измерения в квадрат.

Варианты обозначения

Понятие используется не только в математике. Оно актуально и для физики.

В связи с разносторонностью применения возникает вопрос, какой буквой обозначается площадь.

В зависимости от дисциплины, в рамках которой применяется изучаемое понятие, становится очевидным ответ, какой буквой алфавита обозначают данную величину.

В таких науках, как физика и математика, используется знак латинского алфавита S. Данная буква имеет произношение {эс}.

Среди вопросов, занимающих умы студентов высших учебных заведений, присутствует тема: как обозначить данную величину нескольких геометрических объектов. В данном случае в письменном варианте применяются нижние индексы. Среди значений, используемых в индексной системе обозначений, присутствуют числа.

Примером выступает обозначение S1, S2, S3. Также считается допустимым применение сокращенных наименований геометрических объектов, по отношению к которым производится числовое измерение. Так, при изучении треугольников для сокращенного названия используются наименования вершин, обозначенные латинскими буквами. В качестве примера могут быть SAOB, SCLE, SOME.

Актуальным для учащихся является вопрос, как пишется в физике площадь. Следует отметить, что данным понятием характеризуется поперечное сечение. Считается допустимым использовать для уточненного обозначения нижний индекс. Сохраняется возможность написания простых чисел в индексной системе.

Вопрос, как пишется в строительной механике и сопромате данная величина, заставляет задуматься студентов. В данных дисциплинах под буквой латинского алфавита S подразумевается обозначение статического момента. Так выражается площадь по отношению к рассматриваемой оси. В качестве символа, обозначающего данный показатель, используется буква латинского алфавита A или F.

В словаре Фасмера Макса

Состав и особенности производства

Название «полиэстер» объединяет целую группу тканей, вырабатываемых из синтетических волокон (полиэстеры или полиэфиры). Сырье получают путем переработки продуктов нефтехимии.

В процессе производства из расплавленной полимерной массы формируют нити различной толщины. Затем волокна подвергают специальной обработке для придания им определенных свойств (мягкости, шелковистости, пластичности, прочности).

В зависимости от толщины нитей и способов их отделки получают материал разной плотности и фактуры. Довольно часто для улучшения свойств тканей полиэстер используют в смесях с натуральными и искусственными волокнами.

Принцип расчета площади прямоугольника

Чтобы вычислить площадь прямоугольника, мы посчитаем количество единиц областей, которые содержит прямоугольник:

В прямоугольнике выше 12 квадратов по 1 см². Его площадь составляет 12 см² (4 х 3).

Примечание. В этом расчете длина L и ширина l прямоугольника должны быть выражены в одной и той же единице длины. Результат будет выражен в той же единице измерения, возведенной в квадрат. Например, если длина прямоугольника выражена в метрах, ширина также должна быть выражена в метрах, а результат формулы для расчета площади прямоугольника даст результат в квадратных метрах (м²).

Площадь прямоугольника эквивалентна его территории. Территория — это термин, используемый для обозначения меры площади земли (мы используем единицу измерения гектар, а не м²). Гектар — это метрическая мера земельной площади, равная 10 000 м2.

Самые крупные и полноводные реки России и их значение

Формулы площади квадрата

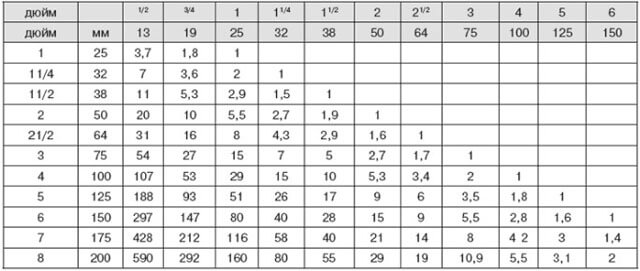
Скачать онлайн таблицу

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.

Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики. Лето  —  прекрасное время, чтобы заниматься ей с удовольствием, в комфортном темпе, без контрольных и оценок за четверть, валяясь дома на полу или за городом на травке.

Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой. Наши преподаватели понятно объяснят что угодно  —  от дробей до синусов —  и ответят на вопросы, которые бывает неловко задать перед всем классом.

Как найти площадь многоугольника

Все, что имеет больше двух углов, является многоугольником, в том числе и треугольник. Рассмотрим, как найти площадь многоугольников.

1

Как найти площадь многоугольника – треугольник

• S = 1/2×h×b, где h – высота, а b – сторона.
• S = 1/2 a×b×sinα, где а и b – стороны треугольника, а sinα – синус угла между ними.
• S = √p×(p-a)×(p-b)×(p-c), где p – половина периметра, а, b, c – стороны. Если известны все стороны треугольника, то найти площадь можно именно по этой формуле.
• S = r×p, где r – радиус вписанной окружности, а p – половина периметра. Если в треугольник вписана окружность, то для нахождения площади можно использовать эту формулу.
• S = abc/4R, где a, b, c – стороны треугольника, а R – радиус описанной окружности. Если треугольник вписан в окружность, для нахождения площади треугольника можно использовать эту формулу.

Прямоугольный треугольник

• S = 1/2×ab, где a и b – катеты прямоугольного треугольника.
• S = d×e, где d и e отрезки гипотенузы, образованные при касании вписанной окружности об гипотенузу.
• S = (p-a)×(p-b), где p – половина периметра, а и b – катеты.

Равнобедренный треугольник

• S = 1/2×a²×sina, где а – бедро треугольника, sina же – угол между бедрами.
• S = b²/4tgα/2, где b – основание треугольника, а tgα – угол между бедрами.

Равносторонний треугольник

• S = √3×a²/4, где а – сторона треугольника (любая, так как в равностороннем треугольнике все стороны равны).
• S = 3√3×R²/4, где R – радиус окружности, в которую вписан треугольник.
• S = 3√3×r², где r – радиус окружности, которая вписана в треугольник.
• S = h²/√3, где h – высота равностороннего треугольника.

2

Как найти площадь многоугольника – квадрат

• S = a², а – сторона квадрата. Так как все стороны квадрата равны, достаточно умножить одну его сторону на другую.
• S = d²/2, где d – диагональ квадрата.

3

Как найти площадь многоугольника – прямоугольник

• S = a×b, где a и b – стороны прямоугольника. Так как противолежащие стороны в прямоугольнике равны, достаточно умножить одну его сторону (длину) на не противолежащую, перпендикулярную сторону (ширину).
• S = a²+b²=c², где a – ширина, b – длина, а c – диагональ. Диагональ делит прямоугольник на два прямоугольных треугольника и если в условии задачи дана одна сторона прямоугольника и его диагональ, несложно будет найти и третью сторону, использую теорему Пифагора. После того как мы найдем эту сторону, ищем площадь по стандартной формуле a×b. Пример: Ширина прямоугольника – 3см, диагональ – 5 см. Найти площадь. Пишем 3² + x² = 5².  x² = 16 => x = 4. S = a×b = 3×4=12. Ответ: S прямоугольника = 12см²

4

Как найти площадь многоугольника – трапеция

• S = (a+b)×h/2, где a – маленькое, b – большое основание трапеции, h – высота.
• S = h×m, где h – высота, m – средняя линия трапеции, равная половине суммы оснований – 1/2×(a+b).
• S = 1/2×d1×d2×sinα, где d1 и d2 – диагонали трапеции, а sinα – синус угла между ними.
• S = a+b/2×√c²-((b-a)²+c²-d²/2(b-a))², где a и b – основания трапеции, c и d – остальные две стороны.

S = 4r²/sinα, где r – радиус вписанной окружности, а sinα – синус угла между стороной и основанием.

5

Площадь правильного многоугольника

• S = r×p = 1/2×r×n×a, где r – радиус вписанной окружности, p – половина периметра. Для того чтобы найти площадь любого правильного многоугольника, нужно разбить его на равные треугольники с общей вершиной в центре вписанной окружности.
• S = n×a²/4tg(360°/2n), где n – число сторон правильного многоугольника, а – длина стороны.Также вычислить площадь правильного многоугольника поможет данный онлайн сервис. Просто вставьте нужное значение и получите ответ.

6

Площадь неправильного многоугольника

Площадь неправильного многоугольника можно найти с помощью координат его вершин. Если в условии задачи даны вышеупомянутые координаты, то выполняем следующее:

• Составляем таблицу указывая букву, обозначающую вершину и соответствующие координаты (x; y).
• Умножаем значение x одной вершины на значение y второй и так далее.
• Складываем все значение, получаем какое-то число.

Составляем точно такую таблицу, по такому же принципу умножаем y координату одной вершины на x координату второй, складываем получившиеся значения.

От суммы значений первой таблицы отнимаем сумму значений второй таблицы.

Полученное число делим на 2 и тем самым находим площадь неправильного многоугольника.

Первая полоса

Беременность

Как не набрать лишний вес во время беременности

Объем и площадь здания жилого и общественного. Общая, расчетная, полезная…

Расчет площади пола в комнате неправильной формы

У комнат, имеющих неправильную форму, рассчитать площадь намного сложнее. Сложности добавляют такие элементы, как арки, ниши в форме полукруга, скошенные стены и т. д. По сути, принцип расчета тот же – нужно разбить помещение на несколько ровных фигур и высчитать площадь каждой отдельно, а потом суммировать. Но площадь круга или треугольника считается уже по другим формулам.

Пол неправильной формы

Например, площадь треугольника высчитывается так: длина основания умножается на высоту треугольника и делится на 2.

Расчет площади комнаты неправильной формы

Площадь многоуровневых полос посчитать не так сложно, как кажется. Просто считаются площади отдельных сегментов и суммируются. Если ступени необходимо отделать таким же напольным материалом, как и остальной пол, то достаточно измерить площадь боковой части каждой ступени и приплюсовать к общей цифре.

Если комната имеет формулу трапеции, то высчитать ее площадь можно без дележки помещения на простые фигуры. Формула трапеции вычисляется так: длина верхней границы (более короткой стороны – а) суммируется с длиной нижней границы (b), затем умножается на высоту трапеции (h) и полученный результат делится на два. Площадь четырехугольника с равными сторонами рассчитать можно по формуле: S = а (длина длинной стороны) х h (высота четырехугольника).

Расчет площадей разных геометрических фигур

Формулы расчетов

Если треугольник не прямой, то рассчитать его площадь можно с помощью формулы Герона

Как рассчитать площадь комнаты — задача для первоклассников

Что может быть про­ще рас­че­та пло­ща­ди пря­мо­уголь­ни­ка? Ведь это самая пер­вая и про­стая зада­ча из учеб­ни­ка гео­мет­рии для пер­во­го класса.

• Изме­ре­ние про­во­дим при помо­щи стро­и­тель­ной рулет­ки с фик­са­то­ром, жела­тель­но у плин­ту­сов, так как если будем делать это посре­дине ком­на­ты, может полу­чить­ся погреш­ность. Жела­тель­но при­сут­ствие помощ­ни­ка, кото­рый будет при­дер­жи­вать один конец рулет­ки. В про­тив­ном слу­чае мож­но закре­пить её каким-то тяжё­лым пред­ме­том или заце­пить за край плинтуса.
• Если дли­на изме­ря­ю­щей лен­ты недо­ста­точ­на, замер при­дёт­ся про­во­дить поэтап­но, фик­си­руя лен­ту и про­став­ляя мет­ки. Затем сум­ми­ру­ем участ­ки дли­ны по про­став­лен­ным мет­кам и полу­ча­ем общий размер.

Напри­мер, дли­на ком­на­ты 5 м, а шири­на — 4 м. Пере­мно­жим эти две циф­ры, полу­ча­ем пло­щадь ком­на­ты — 20 м2 .

Как измерить площадь помещения с нишей

Услож­ним зада­чу: допу­стим в поме­ще­нии име­ет­ся пря­мо­уголь­ная ниша. В этом слу­чае раз­би­ва­ем ком­на­ту на два пря­мо­уголь­ни­ка боль­шой и малень­кий. Изме­рить нуж­но будет две сто­ро­ны боль­шо­го и две сто­ро­ны малень­ко­го прямоугольника:

• дли­ну мень­шей сто­ро­ны ком­на­ты (рас­сто­я­ние до ниши) а1;
• шири­ну ком­на­ты — b1;
• дли­ну и шири­ну ниши а2 и b2 .

Пло­щадь ком­на­ты будет рав­но сум­ме най­ден­ных пло­ща­дей двух пря­мо­уголь­ни­ков: S = а1* b1   + а2 * b2.

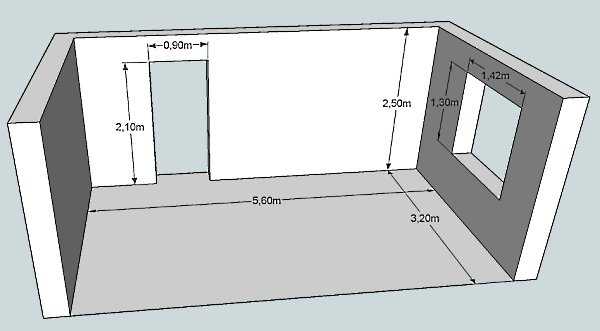
Рас­счи­та­ем пло­щадь ком­на­ты на рисун­ке ниже.

Здесь: а1 = 4.35 м; b1 = 5 м; а2 = 2.65 м; b2 = 2.5 м.

S = 4.35 * 5 + 2.65 * 2.5 =21.75 +6.625 = 28.375 м2.

Как рассчитать площадь комнаты любой формы

Прин­цип рас­че­та оди­на­ков для поме­ще­ний любой формы:

Для вычис­ле­ний доста­точ­но знать сле­ду­ю­щие формулы:

• S пря­мо­уголь­ни­ка = a * b (1), здесь и далее а и b — дли­на и шири­на помещения.
• S пря­мо­уголь­но­го тре­уголь­ни­ка (это поло­ви­на пря­мо­уголь­ни­ка), то есть S тре­уг. = a * b /2 (2);
• S кру­га = π*r2 (или π*d2 / 4) (3) , где π = 3.14, r и d — ради­ус и диа­метр окружности;
• S полу­кру­га = π*r2 /2 (4);
• S тра­пе­ции с осно­ва­ни­я­ми а, b и высо­той h: S трап. = (а + b)/2 * h (5).

Зачем проводить расчет площади комнаты?

Любой ремонт не может начинаться без точных знаний о размерах комнаты. Чтобы посчитать количество обоев или панелей, нужно узнать размеры и площадь стен, для приобретения достаточного количества потолочной плитки снимаются мерки с потолка. Конечно, для закупки в требуемых объемах напольного покрытия также придется постараться и узнать значение площади всего пространства пола.

Для чего могут пригодится расчеты площади

Со снятием мерок с помещения и определением площади основания сталкивается каждый человек, который решил самостоятельно начать ремонт. Если владелец жилого помещения обратился за помощь к специалистам, то ему ни во что вникать не придется – мастера все сделают сами. Однако все же многие решаются на проведение ремонтных работ своими руками. Это позволяет значительно сэкономить деньги, затраченные на ремонт.

Для ремонта необходимо точно знать размеры комнаты

Основные причины необходимости определения площади пола следующие:

• ремонт или первичная укладка напольного покрытия;
• заливка свежей стяжки;
• обустройство системы лаг;
• окрашивание пола;
• нанесение на пол других строительных материалов;
• определение размера жилой площади при оформлении документов либо покупке/продаже квартиры или дома;
• определение соответствия помещения плану комнат;
• подбор мебели по габаритам;
• составление плана комнаты для проведения дальнейших работ;
• оценка стоимости работы специалистов и других затрат.

Не всегда измерение площади пола оказывается простой процедурой

В основном, знание площади пола требуется для того, чтобы высчитать нужное для отделки количество строительных материалов, которые будут использованы при работе. Например, объем цементной смеси для заливки стяжки, количество наливного пола или пачек ламината и т. д.

Виды напольного покрытия

Определение понятия площади

Множество измеримо по Жордану, если внутренняя мера Жордана равна внешней мере Жордана

Площадь — функция, которая обладает следующими свойствами:

• Положительность, то есть площадь неотрицательна;
• Аддитивность, то есть площадь фигуры равна сумме площадей составляющих её фигур без общих внутренних точек;
• Инвариантность, то есть площади конгруэнтных фигур равны;
• Нормированность, то есть площадь единичного квадрата равна 1.

Из данного определения площади следует её монотонность, то есть площадь части фигуры меньше площади всей фигуры.

Первоначально определение площади было сформулировано для многоугольников, затем оно было расширено на квадрируемые фигуры. Квадрируемой называется такая фигура, которую можно вписать в многоугольник и в которую можно вписать многоугольник, причём площади обоих многоугольников отличаются на произвольно малую величину. Такие фигуры называются также измеримыми по Жордану. Для фигур на плоскости, не состоящих из целого количества единичных квадратов, площадь определяется с помощью предельного перехода; при этом требуется, чтобы как фигура, так и её граница были кусочно-гладкими. Существуют неквадрируемые плоские фигуры. Предложенное выше аксиоматическое определение площади в случае плоских фигур обычно дополняют конструктивным, при котором с помощью палетки осуществляется собственно вычисление площади. При этом для более точных вычислений на последующих шагах используют палетки, у которых длина стороны квадрата в десять раз меньше длины у предыдущей палетки.

Площадь квадрируемой плоской фигуры существует и единственна. Понятие площади, распространённое на более общие множества, привело к определению множеств, измеримых по Лебегу, которыми занимается теория меры. В дальнейшем возникают более общие классы, для которых свойства площади не гарантируют её единственность.

Под площадью в обобщённом смысле понимают численную характеристику k-мерной поверхности в n-мерном пространстве (евклидовом или римановом), в частности, характеристику двумерной поверхности в трёхмерном пространстве.

Расчёт площади пола, потолка и стен квартиры

В процессе ремонта, для того чтобы рассчитать точное количество необходимого материала и стоимость отделочных работ в первую очередь нужно вспомнить о том, как определить квадратный метр стены, вычислить площадь полов и потолка. Все эти вычисления будут зависеть не только от формы комнаты, но и от наличия окон и дверей. В том случае если комната прямоугольная, то вычисления квадратного метра будет выполняться по следующим формулам:

Для того чтобы узнать площадь пола и потолка требуется умножить ее длину на ширину; Для вычисления периметра, то есть, чтобы узнать общую длину стен нужно длину и ширину сложить, а потом умножить на два;

Чтобы выполнить расчет площади стен комнаты потребуется умножить периметр на высоту и вычесть из полученного результата площадь дверных и оконных проемов. Но так как большинство стен оснащены окнами или дверью, то для того чтобы посчитать ее квадратные метры необходимо пользоваться формулой. Рассчитать кв.м. можно по следующей схеме:Площадь стены = периметр х высоту – ширина проема х на высоту.

Несколько советов

• Нужно при проведении расчётов все цифры наносить на план. Таким образом сохранится не только результат, но и промежуточные вычисления, которые могут пригодится при проведении ремонтных работ в будущем. 
• При вычислении площади нужно учитывать, что не всегда необходима полная величина. Например, обои могут клеить не только на всю стену, а на их часть. Класть плитку могут до потолка либо только до определённой высоты. Поэтому нужно точно определить, как высчитать квадратуру дома с учётом конкретного плана ремонта. 

Как сделать замеры – можно посмотреть в видеоролике:

Коротко о главном

Для того, чтобы точно знать, сколько необходимо стройматериалов для проведения работ, нужно учитывать площади стен, пола и потолка, а также нормы расхода стройматериалов. Среднюю величину расхода можно узнать, спросив у продавцов, а квадратуру дома необходимо измерить самостоятельно. Для этого нужно воспользоваться знаниями из элементарной геометрии. При вычислении площади сложных фигурных поверхностей их разбивают на простые части, делают необходимые вычисления, затем суммируют их. 

Характеристики понятия

Площадь имеет несколько характеристик:

• Положительность. Площадь не может быть отрицательной, как не может быть отрицательным пространство. Есть единственный случай, когда площадь стремится к нулю: измерение площади точки.

• Нормируемость.

  Что это значит? Это значит, что у площади есть какая-то норма, с которой и сравнивают поверхность любой фигуры. Норма площади это квадрат со сторонами 1 на 1. Если это квадрат со сторонами 1 на 1 см, то единица измерения площади будет называться см квадратный и т.д.

• Если две фигуры объединить, так, что они не будут иметь общих внутренних точек, то есть совместить фигуры по какой-либо стороне, то площадь получившейся фигуры будет равна сумме площадей двух изначальных фигур.

На практике площадь можно определять с помощью палетки или специального измерительного прибора – планиметра.

Как считают объем и площадь здания

Единицы измерения площади

В одном квадратном сантиметре сто квадратных миллиметров

Метрические единицы

• Квадратный метр, производная единица Международной системы единиц (СИ); 1 м² = 1 са (сантиар);
• Квадратный километр, 1 км² = 1 000 000 м²;
• Гектар, 1 га = 10 000 м²;
• Ар (сотка), 1 а = 100 м²:
• Квадратный дециметр, 100 дм² = 1 м²;
• Квадратный сантиметр, 10 000 см² = 1 м²;
• Квадратный миллиметр, 1 000 000 мм² = 1 м²;
• Барн, 1 б = 10−28 м².

Русские устаревшие

• Квадратная верста = 1,13806 км²
• Десятина = 10925,4 м²
• Копна = 0,1 десятины — сенные покосы мерили копнами
• Квадратная сажень = 4,55224 м²

Мерами земли при налоговых расчётах были выть, соха, обжа, размеры которых зависели от качества земли и социального положения владельца. Существовали и различные местные меры земли: коробья, верёвка, жеребья и др.

Другие

• Рай = 1600 м² (40 м × 40 м).
• Квадратный парсек
• Планковская площадь (SP,ℓP2{\displaystyle S_{P},{\ell }_{P}^{2}}) ≈ 2,612099 · 10−70 м2

Вычисление площади прямоугольной комнаты

Помещение, не имеющее никаких, даже небольших, выступов и ниш или, попросту говоря, прямоугольное – самый простой вариант для снятия мерок и подсчета значений площади. Здесь достаточно вспомнить самую простую формулу из курса математики – как рассчитывается площадь такой фигуры, как прямоугольник. Для этого необходимо измерить лишь ширину (А) и длину комнаты (B). Таким образом, мы получаем, что S (площадь) будет равна значению, которое будет получено в результате перемножения двух показателей А и В.

Расчет площади прямоугольной комнаты

Результаты всех измерений указываются в метрах. После запятой указываются сантиметры. Например, длина стены получилась 376 см, тогда получается (в 1 м – 100 см), что длина этой стены будет равна 3 м 76 см.

Меряем прямоугольный пол

Если в комнате есть камин, то нужно посчитать его площадь и отнять от получившейся цифры. Ведь под камином напольное покрытие укладываться не будет. Конечно, если речь не идет о демонтаже этого сооружения.