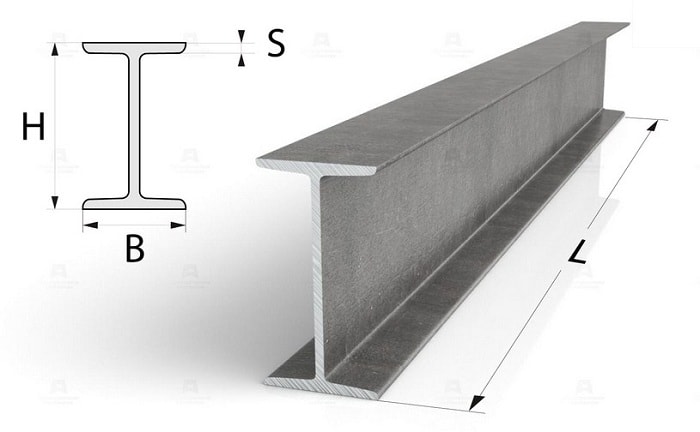
Модуль юнга

Как определить модуль упругости стали

Выяснить модули упругости для различных марок стали можно несколькими путями:

1. по справочным данным из таблиц;
2. экспериментальными методами для небольшого образца;
3. расчетными методами, зная необходимые данные.

Жесткость стали зависит от ее химического состава и вида кристаллической решетки, от плотности, достигнутой в результате обработки. Прочность же ее конструкций определяется такими важными факторами, как параметры изделия, в том числе габариты, эксплуатационные нагрузки, и их длительность. При расчетах, выполняемых по нормированным методикам, результат осознанно завышают, чтобы предупредить возможные аварии и поломки.

Тем не менее, устойчивость стали к деформации определяется изначально ее маркой, то есть наличием примесей в сплаве.

В таблице приведены модули упругости стали наиболее популярных марок, а модуль сдвига ее составляет – 80-81 ГПа.

Сталь	Модуль (Е), ГПа
углеродистая	195-205
легированная	206-235
Ст.3, Ст.5	210
сталь 45	200
25Г2С, 30ХГ2С	200

Из таблицы видно, что наименьшее значение прочности у стали 45, 25Г2С, 30ХГ2С, а у нержавеющей стали самое высокое – 235 ГПа.

Экспериментальный метод определения заключается в определении относительного удлинения небольшого стального образца на установке, с последующим расчетом.

В основе метода лежит заключение, что растяжение образца стали до предела упругости, подчиняется закону Гука (1). Зная приложенную силу (F) и площадь детали (А), выяснив ее удлинение (Δl) можно рассчитать Е:

Расчеты ведут в мм и МПа.

Для проектирования конструкций необходимо всегда знать или просчитывать не менее двух разных модулей упругости. Исходя из коэффициента жесткости можно перейти к другим видам сопротивления к воздействию извне для стали: упругости при изгибе и объемной.

Все твердые тела, как кристаллические, так и аморфные, имеют свойство изменять свою форму под воздействие приложенной к ним силы. Другими словами, они подвергаются деформации. Если тело возвращается к исходным размерам и форме после того, как внешнее усилие прекращает свое воздействие, то его называют упругим, а его деформацию считают упругой. Для любого тела существует предел приложенного усилия, после которого деформация перестает быть упругой, тело не возвращается в исходную форму и к исходным размерам, а остается в деформированном состоянии или разрушается. Теория упругих деформаций тел была создана в конце 17 века британским ученым Р. Гуком и развита в трудах его соотечественника Томаса Юнга. В их честь Гука и Юнга были названы соответственно закон и коэффициент, определяющий степень упругости тел. Он активно применяется в инженерном деле в ходе расчетов прочности конструкций и изделий.

Описание и характеристики единицы измерения

Наименование величины степени жесткости было дано по имени его создателя — английского известного физика, который проводил исследования в области сжатия и растяжения различных жестких материалов, а также в процессах, которые проходят при механическом воздействии. О модуле Юнга справедливо упомянуть следующее:

• это такая единица измерения, которая в цифровом выражении показывает продольную упругость материала какой-либо конструкции;
• эта величина выражает в числах свойства конкретной материи;
• отображает характер его деформации в продольном направлении при оказываемым воздействии.

А если совсем просто, то эта единица измерения просто показывает, насколько жесткий конкретный материал.

Буква Е является обозначением модуля Юнга. Согласно отечественной системе расчетов, измерение этой величины происходит в Паскалях. При этом Международная система единиц высчитывает эту величину в ньютонах, умноженных на метр в квадрате (СИ).

Модуль продольной жёсткости применяется при разного рода вычислениях во время проверки структур веществ на степень реакции при сжатии, растяжении, перегибании.

Следует отметить, что наибольшее количество конструкционных материалов, которые используют в таких расчетах, имеет довольно высокий показатель модуля Юнга. Чаще всего его значение начинается от отметки 109 Паскалей. В связи с этим в большинстве случаев для удобства записывания вычислений и самих расчетов применяют префикс «гига» (ГПа).

https://youtube.com/watch?v=aSyofv5gY3I

https://youtube.com/watch?v=kaZz1ABpUsc

Упругие деформации. Модуль Юнга и коэффициент Пуассона. Энергия упругой деформации.

Все тела деформируемы. Изменения, вызванные действиями приложенных сил, при которых тела меняют форму и объем – деформации.

 Упругие деформации – деформации, которые исчезают, после прекращения действия приложенной силы.

Пластические деформации (остаточные деформации) – деформации, которые сохраняются в теле (частично или полностью) после прекращения действия приложенной силы.

Если напряжение (сила, отнесенная к единице площади) не превышает некоторой величины (предел упругости), то деформация будет упругой.

Идеально упругие тела – тела, которые могут претерпевать только упругие деформации. Для таких тел существует однозначная зависимость между силами и вызываемыми ими деформациями.

Малые деформации – деформации, которые подчиняются закону Гука, согласно которому

деформации пропорциональны силам, их вызывающимизотропныеанизотропные

Пусть есть два стержня. Один сжимаем, а другой сдавливаем с силой  (как на рисунке). Перпендикулярно к оси стержня проведем сечение .  Для равновесия стержня , на его нижнее основание должна действовать сила . Нижняя и верхняя части стержня действуют друг на друга с равной силой , т.к. они деформированы. Отношение силы к площади поперечного сечения ­– напряжение.

Натяжение – напряжение при натяжении, .

Давление – напряжение при сжатии , где  площадь сечения. Давление – отрицательное напряжение и наоборот .

 – длина недеформированного стержня.  – приращение длины, после приложения силы . Значит полная длина .  – относительное удлинение стержня (если  – относительное сжатие).

Для малых упругих деформаций натяжение  (давление ) пропорционально относительному удлинению (относительному сжатию) —

  (),

где  – модуль Юнга (постоянная, зависящая только от материала стержня и его физического состояния).

Модуль Юнга – натяжение, которое необходимо приложить к стержню, чтобы его длина увеличилась в два раза. А две формулы выше – закон Гука.

Вычислим упругую энергию растянутого стержня. Приложим к стержню растягивающую силу  и будем постепенно (непрерывно и медленно) увеличивать ее от  до . Удлинение будет меняться от  до . По закону Гука ,

где  – коэффициент упругости.

Вся работа по растяжению стержня пойдет на увеличение его упругой энергии . Т.к. в конечном состоянии , то , то для энергии получим .

Под действием растягивающей или сжимающей силы  изменяются не только продольные, но и поперечные размеры стержня. Если сила ­ растягивающая, то поперечные размеры стержня уменьшаются. Если она сжимающая, то они увеличиваются.

 – коэффициент Пуассона.

Он зависит только от материала рассматриваемого тела. Модуль Юнга и коэффициент Пуассона полностью характеризуют упругие свойства изотропного материала. Все остальные упругие деформации можно выразить через эти коэффициенты.

Post Views: 4 220

Приложения

Удельная жесткость при растяжении

Использовать определенную жесткость при растяжении несложно. И жесткость при растяжении, и общая масса для данной длины прямо пропорциональны площади поперечного сечения . Таким образом, характеристики балки при растяжении будут зависеть от модуля Юнга, деленного на плотность .

Удельная жесткость на изгиб и изгиб

Определенная жесткость может использоваться при проектировании балок, подверженных изгибу или продольному изгибу по Эйлеру , поскольку изгиб и продольный изгиб обусловлены жесткостью. Однако роль, которую играет плотность, меняется в зависимости от ограничений задачи.

Балка с фиксированными размерами; цель — снижение веса

Изучая формулы для продольного изгиба и прогиба , мы видим, что сила, необходимая для достижения заданного прогиба или изгиба, напрямую зависит от модуля Юнга .

Рассматривая формулу плотности , мы видим, что масса балки напрямую зависит от плотности.

Таким образом, если размеры поперечного сечения балки ограничены, а основной целью является снижение веса, характеристики балки будут зависеть от модуля Юнга, деленного на плотность .

Балка с фиксированным весом; цель — повышение жесткости

Напротив, если вес балки фиксирован, ее размеры в поперечном сечении не ограничены и повышенная жесткость является основной целью, характеристики балки будут зависеть от модуля Юнга, деленного либо на квадрат плотности, либо на куб. Это связано с тем, что общая жесткость балки и, следовательно, ее сопротивление продольному изгибу Эйлера под действием осевой нагрузки и прогибу под действием изгибающего момента прямо пропорциональны как модулю Юнга материала балки, так и второму моменту площади ( момент инерции области) балки.

Сравнение списка моментов инерции площадей с формулами для площади дает соответствующее соотношение для балок различной конфигурации.

Площадь поперечного сечения балки увеличивается в двух измерениях.

Рассмотрим балку, площадь поперечного сечения которой увеличивается в двух измерениях, например сплошная круглая балка или сплошная квадратная балка.

Комбинируя формулы площади и плотности , мы можем видеть, что радиус этого луча будет изменяться приблизительно обратно пропорционально квадрату плотности для данной массы.

Изучая формулы для момента инерции площади , мы можем увидеть, что жесткость этой балки будет изменяться приблизительно как четвертая степень радиуса.

Таким образом, второй момент площади будет изменяться приблизительно как величина, обратная квадрату плотности, и характеристики луча будут зависеть от модуля Юнга, деленного на квадрат плотности .

Площадь поперечного сечения балки увеличивается в одном измерении

Рассмотрим балку, площадь поперечного сечения которой увеличивается в одном измерении, например, тонкостенная круглая балка или прямоугольная балка, высота, но не ширина которой изменяется.

Комбинируя формулы площади и плотности , мы можем видеть, что радиус или высота этого луча будет изменяться приблизительно обратно пропорционально плотности для данной массы.

Изучая формулы для момента инерции площади , мы можем видеть, что жесткость этой балки будет изменяться приблизительно как третья степень радиуса или высоты.

Таким образом, второй момент площади будет изменяться приблизительно как величина, обратная кубу плотности, и характеристики луча будут зависеть от модуля Юнга , деленного на куб плотности .

Однако следует соблюдать осторожность при использовании этой метрики. В конечном итоге тонкостенные балки ограничиваются местным изгибом и продольным изгибом при

Эти режимы потери устойчивости зависят от свойств материала, отличных от жесткости и плотности, поэтому кубическая метрика жесткости над плотностью в лучшем случае является отправной точкой для анализа. Например, большинство древесных пород оцениваются по этому показателю лучше, чем большинство металлов, но многие металлы могут быть сформированы в полезные балки с гораздо более тонкими стенками, чем это может быть получено с древесиной, учитывая большую уязвимость древесины к местному короблению. Характеристики тонкостенных балок также можно значительно изменить за счет относительно незначительных изменений геометрии, таких как фланцы и ребра жесткости.

Обратите внимание, что предел прочности балки на изгиб зависит от предельной прочности ее материала и модуля упругости сечения , а не от жесткости и второго момента площади. Однако его прогиб и, следовательно, его сопротивление продольному изгибу по Эйлеру будут зависеть от этих двух последних значений.

Что представляет собой печь-голландка

Первые голландские печи появились в 15 веке. Внешний вид и размер немного изменились, но концепция осталась прежней: это компактный отопительно-варочный прибор, который может вписаться в помещение любого размера и великолепно справится со своей задачей.

Небольшие габариты конструкции объясняются небольшими размерами домов в Нидерландах. Иногда требовалось поставить печь в помещения до 10 кв. м. Города в северной Голландии — густонаселённые, местный климат — холодный и суровый. Поэтому печи здесь ставили самого высокого качества.

Высокие налоги на земельные участки заставили местных жителей строить узкие и высокие дома. Для таких проектов нужны особые конструкции печей. Голландки именно так и выглядят: вытянуты вверх на большую высоту. Одна печка способна отопить два-три этажа домовладения. В самых первых моделях ещё не было колосника и поддувала, варочных панелей тоже не устанавливали. Все эти атрибуты появились со временем. Тем самым КПД стал существенно выше.

Горячие газы в голландской печи идут по шести магистралям: трём подъемным и трём опускным. Колпаковая система аккумулирует горячий воздух и повышает теплоотдачу.

Отличительная особенность первых конструкций — арочный свод, который затем был заменен на стандартную прямоугольную форму топливника.

Есть множество разновидностей схем печи голландки с плитой, которые оборудованы камерами для выпечки хлеба, лежанками, баком для нагрева воды и другими полезными атрибутами.

Но наибольшую популярность имеют печки голландки с плитой.

Общее понятие

Модуль упругости (также известный как модуль Юнга) – один из показателей механических свойств материала, который характеризует его сопротивляемость деформации растяжения. Другими словами, его значение показывает пластичность материала. Чем больше модуль упругости, тем менее будет растягиваться какой-либо стержень при прочих равных условиях (величина нагрузки, площадь сечения и прочее).

В теории упругости модуль Юнга обозначается буквой Е. Является составной частью закона Гука (закона о деформации упругих тел). Связывает напряжение, возникающее в материале, и его деформацию.

Согласно международной стандартной системе единиц измеряется в МПа. Но на практике инженеры предпочитают использовать размерность кгс/см2.

Определение модуля упругости осуществляется опытным путем в научных лабораториях. Суть данного способа заключается в разрыве на специальном оборудовании гантелеобразных образцов материала. Узнав напряжение и удлинение, при котором произошло разрушение образца, делят данные переменные друг на друга, тем самым получая модуль Юнга.

Отметим сразу, что таким методом определяются модули упругости пластичных материалов: сталь, медь и прочее. Хрупкие материалы – чугун, бетон – сжимают до появления трещин.

Дополнительные характеристики механических свойств

Модуль упругости дает возможность предугадать поведение материла только при работе на сжатие или растяжение. При наличии таких видов нагрузок как смятие, срез, изгиб и прочее потребуется введение дополнительных параметров:

• Жесткость есть произведение модуля упругости на площадь поперечного сечения профиля. По величине жесткости можно судить о пластичности уже не материала, а узла конструкции в целом. Измеряется в килограммах силы.
• Относительное продольное удлинение показывает отношение абсолютного удлинения образца к общей длине образца. Например, к стержню длиной 100 мм приложили определенную силу. Как результат, он уменьшился в размере на 5 мм. Деля его удлинение (5 мм) на первоначальную длину (100 мм) получаем относительное удлинение 0,05. Переменная является безразмерной величиной. В некоторых случаях для удобства восприятия переводится в проценты.
• Относительное поперечное удлинение рассчитывается аналогично вышепредставленному пункту, но вместо длины здесь рассматривается диаметр стержня. Опыты показывают, что для большинства материалов поперечное удлинение в 3-4 раза меньше, чем продольное.
• Коэффициент Пуансона есть отношение относительной продольной деформации к относительной поперечной деформации. Данный параметр позволяет полностью описать изменение формы под воздействием нагрузки.
• Модуль сдвига характеризует упругие свойства при воздействии на образец касательных напряжений, т. е. в случае, когда вектор силы направлен под 90 градусов к поверхности тела. Примерами таких нагрузок является работа заклепок на срез, гвоздей на смятие и прочее. По большому счету, модуль сдвига связан с таким понятием как вязкость материла.
• Модуль объемной упругости характеризуется изменением объема материала для равномерного разностороннего приложения нагрузки. Является отношением объемного давления к объемной деформации сжатия. Примером такой работы служит опущенный в воду образец, на который по всей его площади воздействует давление жидкости.

Помимо вышесказанного необходимо упомянуть, что некоторые типы материалов имеют различные механические свойства в зависимости от направления нагрузки. Такие материалы характеризуются как анизотропные. Яркими примерами служит древесина, слоистые пластмассы, некоторые виды камня, ткани и прочее.

У изотропных материалов механические свойства и упругая деформация одинаковы в любом направлении. К ним относят металлы (сталь, чугун, медь, алюминий и прочее), неслоистые пластмассы, естественные камни, бетон, каучук.

Модуль упругости алюминия и алюминиевых сплавов

Модуль упругости = Модуль Юнга

На рисунке можно видеть, что на начальном этапе кривой напряжение-деформация увеличение деформации на единицу увеличения напряжения у алюминия и алюминиевых сплавов происходит намного быстрее, чем у стали – в три раза.

Наклон этой части кривой определяет характеристику материала — модуль упругости (модуль Юнга). Поскольку единица измерения деформации – безразмерная величина, то размерность модуля Юнга совпадает с размерностью напряжения.

Модуль Юнга алюминия составляет примерно одну треть от модуля Юнга стали и для большинства алюминиевых сплавов находится между 65500 и 72400 МПа. См. Модуль упругости различных алюминиевых сплавов

Можно отметить, что при этом алюминиевая балка тех же размеров, что и стальная балка поглощает в три раза больше энергии, но только до тех пор, пока напряжения в алюминиевом сплаве остаются ниже предела упругости.

Жесткость алюминиевых профилей

Стоит отметить, что жесткость конструкционного элемента определяется как произведение модуля упругости материала и момента инерции сечения элемента (E × I) и именно от жесткости зависит прогиб элемента под воздействием изгибающей нагрузки.

Это дает алюминию шанс в соревновании со сталью: прессованные алюминиевые профили могут иметь намного более сложные поперечные сечения и тем самым компенсировать малость модуля упругости алюминия увеличением момента инерции их поперечных сечений. Кроме жесткости на изгиб необходимо учитывать и другие факторы, например, жесткость на кручение.

В результате всего этого сложность поперечного сечения профиля возрастает и часто «съедает» часть ожидаемого выигрыша в весе, который обычно составляет около 50 % вместо возможных 33 %.

Модуль упругости различных материалов

Модули упругости для различных материалов имеют совершенно разные значения, которые зависят от:

• природы веществ, формирующих состав материала;
• моно- или многокомпонентный состав (чистое вещество, сплав и так далее);
• структуры (металлическая или другой вид кристаллической решетки, молекулярное строение прочее);
• плотности материала (распределения частиц в его объеме);
• обработки, которой он подвергался (обжиг, травление, прессование и тому подобное).

Его значение для бронзовых материалов зависит не только от обработки, но и от химического состава:

• бронза – 10,4 ГПа;
• алюминиевая бронза при литье – 10,3 ГПа;
• фосфористая бронза катанная – 11,3 ГПа.

Модуль Юнга латуни на много ниже – 78,5-98,1. Максимальное значение имеет катанная латунь.

Сама же медь в чистом виде характеризуется сопротивлением к внешним воздействиям значительно большим, чем ее сплавы – 128,7 ГПа. Обработка ее также снижает показатель, в том числе и прокатка:

• литая – 82 ГПа;
• прокатанная – 108 ГПа;
• деформированная – 112 ГПа;
• холоднотянутая – 127 ГПа.

Близким значением к меди обладает титан (108 ГПа), который считается одним из самых прочных металлов. А вот тяжелый, но ломкий свинец, показывает всего 15,7-16,2 ГПа, что сравнимо с прочностью древесины.

Для железа показатель напряжения к деформации также зависит от метода его обработки: литое – 100-130 или кованное – 196,2-215,8 ГПа.

Чугун известен своей хрупкостью имеет отношение напряжения к деформации от 73,6 до 150 ГПа, что соответствует от его виду. Тогда как для стали модуль упругости может достигать 235 ГПа.

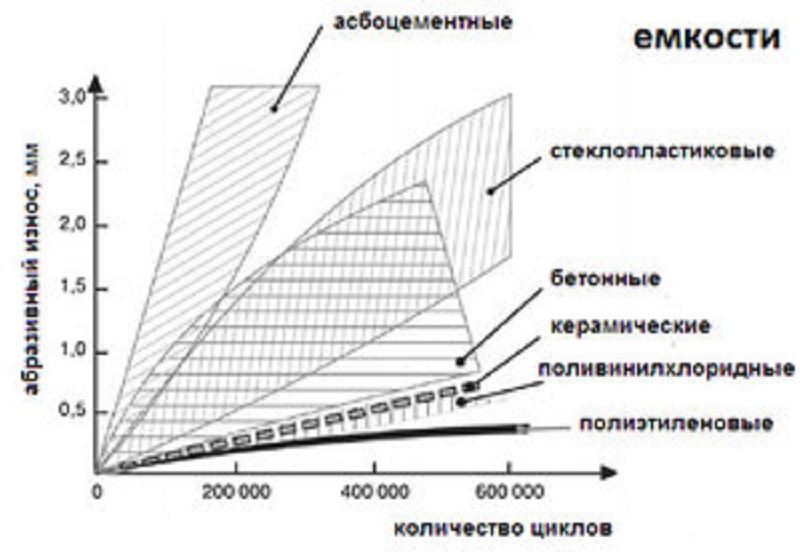
Модули упругости некоторых материалов

На величины параметров прочности влияют также и формы изделий. Например, для стального каната проводят расчеты, где учитывают:

• его диаметр;
• шаг свивки;
• угол свивки.

Интересно, что этот показатель для каната будет значительно ниже, чем для проволоки такого же диаметра.

Стоит отметить прочность и не металлических материалов. Например, среди модулей Юнга дерева наименьший у сосны – 8,8 ГПа, а вот у группы твердых пород, которые объединены под названием «железное дерево» самый высокий – 32,5 ГПа, дуб и бук имеют равные показатели – 16,3 ГПа.

Среди строительных материалов, сопротивление к внешним силам у, казалось бы, прочного гранита всего 35-50 ГПа, когда даже у стекла – 78 ГПа. Уступают стеклу бетон – до 40 ГПа, известняк и мрамор, со значениями 35 и 50 ГПа соответственно.

Такие гибкие материалы, как каучук и резина, выдерживают осевую нагрузку от 0,0015 до 0,0079 ГПа.

Нормативные характеристики бетона: объемный вес, сопротивление, однородность, модуль упругости

Объемный вес бетона и железобетона (в кг/м2)

Вид бетона	Бетон	Железобетон
Тяжелый бетон на гравии или щебне из природного камня (невибрированный)	2300	2400
Тоже, вибрированный или центрифугированный	2400	2500
Тяжелый бетон на кирпичном щебне не невибрированный	1800	1000
То же, вибрированный	2000	2100
Легкий бетон	По фактическому фесу

Объемный вес легкого бетона на керамзите или шлаках составляет (ориентировочно) 1500 —1800 кг/м3, а легкого железобетона на пемзе или туфе — 1100—1500 кг/м3.

При проценте армирования более 3,0 объемный вес железобетона должен быть подсчитан как сумма весов бетона и арматуры на единицу объема конструкции.

Бетон м200 характеристики: нормативные сопротивления (пределы прочности) бетона должны приниматься по табл. 1.

Таблица 1.

Нормативные сопротивления бетона (в кг/см2)

Вид напряженного состоянияние	Условное обозначе	Марка бетона
35	50	75	100	150	200	300	400	500	600
Сжатие осевое (призменная прочность)	RНпр	28	40	60	80	115	145	210	280	350	420
Сжатие при изгибе	RНИ	35	50	75	100	140	180	260	350	440	520
Растяжение	RНр	5	6	8	10	13	16	21	25	28	30
Срез	RНср	8	11	16	20	28	35	47	58	68	77

Величина RНср в СН и П не приведена и в таблице указана ориентировочно.

2. Нормативные сопротивления растяжению бетонов на глиноземистом цементе принимаются с коэффициентом 0,7.

Коэффициенты однородности бетона kб должны приниматься по табл. 2

Таблица 2. Коэффициенты однородности бетона kб

Вид напряженного состояния	Условия приготовления бетона	Марка бетона
35—200	300—600
Сжатие осевое и при изгибе	А	0,60	0,65
Б	0,55	0,60
Растяжение	А	0,45	0,50
Б	0,40	0,45

1. Значения коэффициентов однородности, указанные в строке А, принимаются для бетонов, приготовляемых на бетонных заводах или бетонных узлах, оборудованных механизмами для автоматического дозирования составляющих бетона (вяжущего, фракций заполнителя, воды и добавок) при систематическом контроле прочности и однородности бетона при сжатии.

В остальных случаях значения коэффициеита однородности бетона принимаются по строке Б.

2. При установлении марок бетона пос растяжению и систематическом контроле прочности и однородности бетона при растяжении величины коэффициентов однородности бетона при растяжении, приведенные в табл. 2, повышаются на 10%.

Нормативные модули упругости бетона при сжатии EНδ должны приниматься по табл. 3.

Модуль сдвига для бетона может быть принят

GНδ= 0,425 EНδ

Таблица 3. Нормативные модули упругости бетона при сжатии EНδ (в кг/см2)

Марка бетона	Тяжелый бетон	Легкий бетон
35	—	60000
50	110000	70000
75	155000	95000
100	190000	110000
150	240000	130000
200	290000	150000
300	340000	—
400	380000	—
500	410000	—
600	430000	—

1. Нормативные модули упругости для легких бетонов даны для бетонов на котельных и металлургических шлаках и на керамзите. Модули упругости для легких бетонов на пемзе, туфе и т. п. принимаются по специальным техническим условиям или экспериментальным данным.

2. Нормативные модули упругости для легких бетонов марок 100 и 150 при изготовлении их на кварцевом песке принимаются по табл. 27 с повышением на 40%.

Коэффициент поперечногорасширения бетона может быть принят

в упругой стадии работы γ = 1/6

в стадии разрушения γ = 0

Таблица показателей упругости материалов

Перед тем, как перейти непосредственно к этой характеристике стали, рассмотрим для начала, в качестве примера и дополнительной информации, таблицу, содержащую данные об этой величине по отношению к другим материалам. Данные измеряются в МПа.

Модуль упругости различных материалов

Как можно заметить из представленной выше таблицы, это значение является разным для разных материалов, к тому же показателя разнятся, если учитывать тот или иной вариант вычисления этого показателя. Каждый волен выбирать именно тот вариант изучения показателей, который больше подойдёт ему. Предпочтительнее, возможно, считать модуль Юнга, так как он чаще применяется именно для характеристики того или иного материала в этом отношении.

После того как мы кратко ознакомились с данными этой характеристики других материалов, перейдём непосредственно к характеристике отдельно стали.

Для начала обратимся к сухим цифрам и выведем различные показатели этой характеристики для разных видов сталей и стальных конструкций:

• Модуль упругости (Е) для литья, горячекатанной арматуры из сталей марок, именуемых Ст.3 и Ст. 5 равняется 2,1*106 кг/см^2.
• Для таких сталей как 25Г2С и 30ХГ2С это значение равно 2*106 кг/см^2.
• Для проволоки периодического профиля и холоднотянутой круглой проволоки, существует такое значение упругости, равняющееся 1,8*106 кг/см^2. Для холодно-сплющенной арматуры показатели аналогичны.
• Для прядей и пучков высокопрочной проволоки значение равняется 2·10 6 кГ/см^2
• Для стальных спиральных канатов и канатов с металлическим сердечником значение равняется 1,5·10 4 кГ/см^2, в то время как для тросов с сердечником органическим это значение не превышает1,3·10 6 кГ/см^2 .
• Модуль сдвига (G) для прокатной стали равен 8,4·10 6 кГ/см^2 .
• И напоследок коэффициент Пуассона для стали равен значению 0,3

Это общие данные, приведённые для видов стали и стальных изделий. Каждая величина была высчитано согласно всем физическим правилам и с учётом всех имеющихся отношений, которые используются для выведения величин этой характеристики.

Ниже будет приведена вся общая информация об этой характеристике стали. Значения будут даваться как по модулю Юнга, так и по модулю сдвига, как в одних единицах измерения (МПа), так и в других (кг/см2, ньютон*м2).

Сталь и несколько разных её марок

Значения показателей упругости стали разнятся, так как существуют сразу несколько модулей, которые исчисляются и высчитываются по-разному. Можно заметить тот факт, что в принципе сильно показатели не разнятся, что свидетельствует в пользу разных исследований упругости различных материалов. Но сильно углубляться во все вычисления, формулы и значения не стоит, так как достаточно выбрать определённое значение упругости, чтобы уже в дальнейшем ориентироваться на него.

Кстати, если не выражать все значения числовыми отношениями, а взять сразу и пос, то эта характеристика стали будет равна: Е=200000 МПа или Е=2 039 000 кг/см^2.

Данная информация поможет разобраться с самим понятием модуля упругости, а также ознакомиться с основными значения данной характеристики для стали, стальных изделий, а также для нескольких других материалов.

Следует помнить, что показатели модуля упругости разные для различных сплавов стали и для различных стальных конструкций, которые содержат в своём составе и другие соединения. Но даже в таких условиях, можно заметить тот факт, что различаются показатели ненамного. Величина модуля упругости стали практически зависит от структуры. а также от содержания углерода. Способ горячей или холодной обработки стали также не может сильно повлиять на этот показатель.

Это интересно: Молибден — свойства, формула, применение элемента и сплавы на его основе