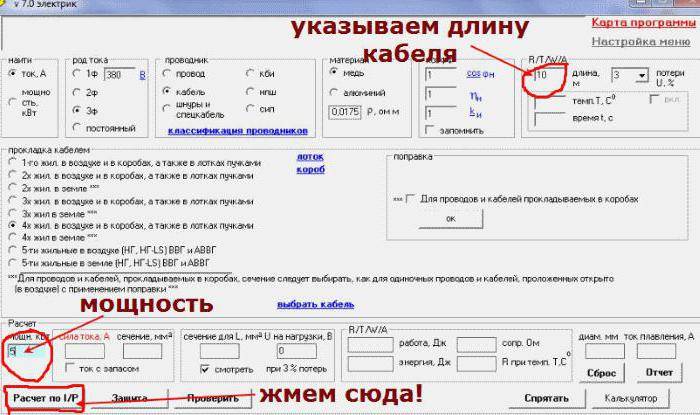
Определение площади сечения проводника по его диаметру

Черчение

Производственные чертежи содержат различные типы изо­бражений — виды, разрезы, сечения.

Сечения и разрезы позволяют выявить внешнюю и внутрен­нюю (рис. 147, а, б) форму детали. Названные изображения по­лучают в результате мысленного рассечения детали секущей плоскостью, положение которой выбирают в зависимости от формы изображаемой детали. Сечения и разрезы дополняют и уточняют геометрическую информацию о предмете и тем самым увеличивают возможности выявления формы изображаемого объекта на чертеже. В некоторых случаях они имеют большую информационную емкость, чем виды. Разрезы и сечения являют­ся проекционными изображениями и выполняются по правилам прямоугольного проецирования.

Рис. 147. Сечение (а) и разрез (б)

Сечение — изображение фигуры, получающейся при мыслен­ном рассечении предмета секущей плоскостью. В сечении пока­зывается только то, что находится в секущей плоскости.

Деталь проецируют на плоскость проекций V (рис. 148, а). Затем ее мысленно рассекают секущей плоскостью в том месте, где необходимо уточнить форму изделия. В секущей плоскости получают фигуру сечения. После этого секущую плоскость (вме­сте с фигурой сечения) мысленно вынимают, поворачивают во­круг вертикальной оси, перемещают параллельно плоскости про­екций и совмещают с плоскостью V так, чтобы изображения вида спереди и фигуры сечения не заслоняли друг друга (рис. 148, б)

Обратите внимание на то, что при таком перемеще­нии секущей плоскости вид спереди находится в проекционной связи с сечением. Полученное изображение фигуры сечения на­зывают сечением, выполненным в проекционной связи

Секущую плоскость с фигурой сечения допускается переме­щать в произвольном направлении, совмещая ее с плоскостью проекций, без учета проекционной связи. Такое сечение называ­ется сечением, выполненным на свободном месте чертежа (рис. 148, в). Сечение можно располагать и на продолжении сле­да секущей плоскости (рис. 148, г). Оно называется сечением, выполненным на продолжении следа секущей плоскости.

Если сечение располагается на продолжении следа секущей плоскости, то сечение не обозначается (см. рис. 148, г). Если се­чение располагается на свободном месте чертежа, то его обозна­чают надписью типа «А — А» (см. рис. 148, б, в).

Если секущая плоскость проходит вдоль оси цилиндрической или фонической поверхности, ограничивающих отверстие или уг­лубление, то их контур на сечении показывают полностью, на­пример изображение углубления конической формы (см. рис. 148).

Для выявления формы некоторых деталей иногда требуется выполнить несколько сечений, которые на чертеже обозначают буквами русского алфавита (рис. 149).

ГОСТ 2.305—68 устанавливает правила изображения и обозначения сечений.

Контуры фигуры сечения детали изображают сплошной ос­новной линией. Внутри этих контуров дают условное графическое обозначение материала детали (табл. 12).

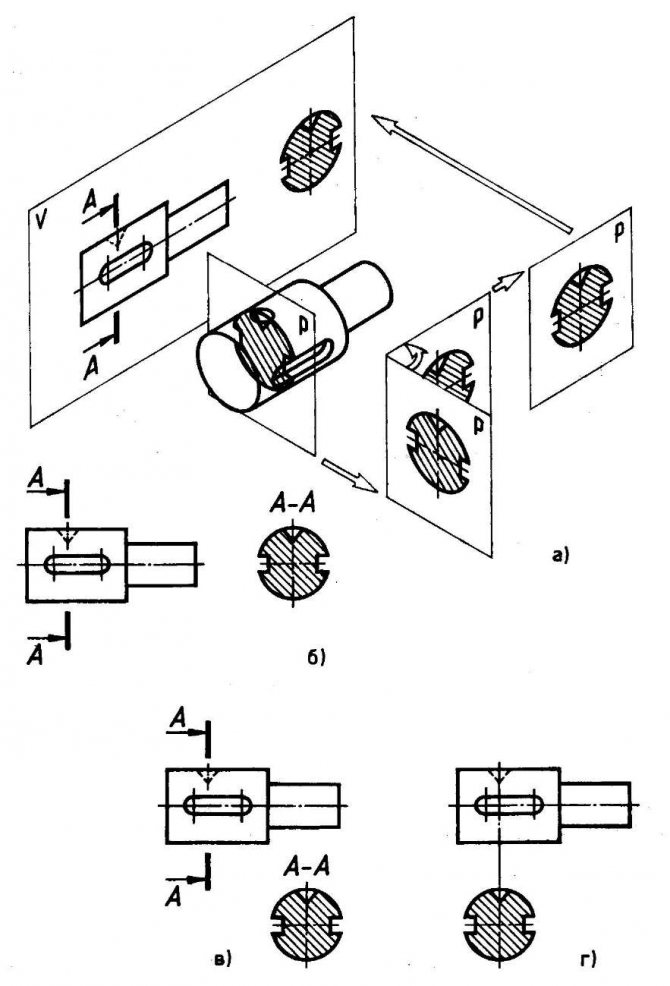
Рис. 148. Сечения:

а — получение сечения; б — сечение, построенное в проекционной связи с видом; в — сечение, выполненное на свободном месте чертежа; г — се­чение, выполненное на продолжении следа секущей плоскости

Рис. 149. Обозначение сечений буквами русского алфавита

12. Графические обозначения некоторых материалов на чертежах

Особенности труб с различными сечениями.

Трубы круглого сечения очень просто очищаются от образовавшегося осадка гидравлическим способом с использованием шаров и цилиндров

По мере того увеличения диаметра трубы круглого сечения, давление грунта и временной внешней нагрузки стремительно увеличиваются. Для уменьшения усилия в стенках труб, своду придают полуэллиптическое сечение.

Иногда может использоваться яйцевидная форма сечения, труба такого сечения способна высокие статические и динамические нагрузки, но такая трубы имеет и недостатки: для монтажа труб с таким сечением необходима большая высота канала и глубина заложения, чем для труб круглого сечения при одинаковой пропускной способности.

Кроме этого, в трубах эллиптического сечения намного быстрее образуется осадок, который отлаживается на стенках. В тех местах, где присутствуют плывуны и грунт очень влажный, могут использоваться трубы лотковой формы. Это позволяет прокладывать канализационные сети на меньшей глубине.

Площадь круга

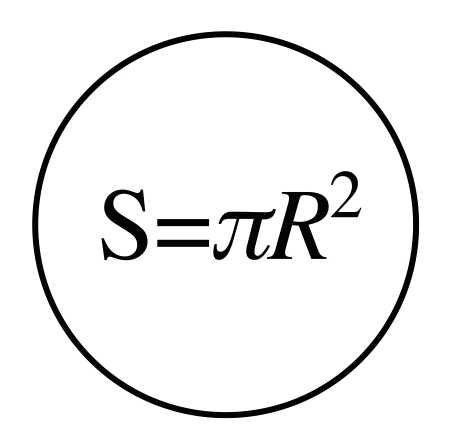
Для того чтобы найти площадь круга, существует формула, которую лучше запомнить:

S=πr2 – это произведение числа пи на квадрат радиуса.

Поскольку радиус тесно связан отношениями с диаметром и длиной окружности, то путем нехитрых замен можно также вычислить площадь круга через диаметрили длину окружности.

Установить Площадь круга на мобильный

Диаметр – это удвоенный радиус, следовательно, подставляя его в формулу вместо последнего, нужно разделить его обратно на два.Длина окружности представляет собой удвоенное произведение радиуса и числа π: P=2πr, обратным методом получаем, что радиус равен длине окружности, разделенной на его множитель.

Данные онлайн калькуляторы предназначены для расчета площади круга. Вычисление происходит по приведенным выше геометрическим формулам, где π считается константой, округленной до 15-го знака после запятой.Определение: Круг- это часть плоскости , ограниченная окружностью, круг является выпуклой фигурой.Результат работы калькулятора так же округляется до аналогичного разряда. Для использования калькулятора расчета площади круга необходимо ввести только значение радиуса, диаметра или окружности круга. Для калькулятора единицы измерения радиуса не имеют значения – результат вычисляется в абсолютном виде. То есть, если значение радиуса задано, например, в сантиметрах, то и вычисленное калькулятором значение площади круга тоже следует интерпретировать как представленное в квадратных сантиметрах.

Первоначальные данные и вычисления

Для начала необходимо сказать о том, что сама конструкция изделий подобного типа фактически является цилиндром. Учитывая это, и следует подбирать специальные формулы, которые известны из начального курса геометрии.

Однако стоит отметить, что сортамент труб круглого сечения по ГОСТу довольно разнообразен и при работе с данными это необходимо учитывать.

Формулы

Обычно площадь круга находится с использованием формулы S= π•R 2 .

• В данном случае под литерой R подразумевают радиус самой трубы, а буква π является константой, равной числу 3.14.
• Однако такая формула площади сечения трубы позволяет получить данные с учетом самих стенок, что может пригодиться только для пробоя отверстий прохождения. Для оценки пропускной способности нужны совершенно другие расчеты.

Учитывая все особенности применяемых материалов, следует получить площадь живого сечения трубы, где во внимание принимается и толщина стенок. Выглядит такая формула так: S= π•(D/2-N) 2
В данной ситуации литера D указывает на внешний диаметр изделия, который легко измерить при помощи линейки или посмотрев в спецификацию

Буква же N означает толщину стенки трубы. Именно ее часто определяет сортамент стальных труб круглого сечения, а получить эту величину можно также из спецификации или же при помощи линейки.

Программы

В современном строительстве расчет площади трубы круглого сечения выполняют с использованием специального программного обеспечения. Обычно мастера применяют полноценные калькуляторы, позволяющие получать самые разнообразные данные, где трубам отводится целая система. Однако существуют и программы, разработанные только для получения этих данных.

Большинство таких калькуляторов разработаны для использования на любых платформах, поэтому их можно установить даже на мобильный телефон, чтобы получить возможность узнать сечение трубы для отопления прямо на месте работы, не прибегая к самостоятельному вычислению.

Стоит отметить, что подобного рода софт может разрабатываться самыми разными компаниями. Поэтому прежде чем начинать его использовать стоит убедиться, что в нем применяется метрическая система измерений. В противном случае можно получить момент сопротивления сечения трубы или другие данные в единицах, которые придется дополнительно обрабатывать.

Область использования

Прежде всего, полученные параметры применяют для того, чтобы установить расход воды в трубе круглого сечения

Это очень важно при работе с дорогими жидкостями или газами, для которых и собирается трубопровод

• Считается, что расчет количества воды по сечению трубы самый точный и при известной величине давления можно получить все самые необходимые данные про систему. Это часто используют на производстве и при создании охладительных систем.
• Если система создается своими руками в бытовых целях, то подобные параметры знать совершенно не обязательно. Однако при разветвленном водопроводе такие вычисления могут пригодиться. (См. также статью Разводка труб: особенности.)

• Стоит отметить, что не достаточно знать все необходимые данные, а нужно еще уметь их применять. Поэтому для сложных проектов стоит нанимать специалистов, хотя их цена порой довольно высока.
• Необходимо сказать о том, что в определенных случаях нужно использовать материалы со строго определенной площадью сечения. Этого требует инструкция по монтажу, основываясь на характеристиках точек потребления или необходимых конечных характеристиках всей системы. (См. также статью Система канализации: особенности.)

Примеры проведения расчетов

Существенную помощь в разборе принципов вычислений и последовательности действий при выполнении расчетов окажут конкретные примеры, с которыми стоит ознакомиться заинтересованным посетителям.

Расчет объема требуемого теплоносителя

Для загородного дома временного проживания нужно рассчитать объем закупаемого пропиленгликоля – теплоносителя не застывающего при температурах до -30°C. Система отопления состоит из печи с рубашкой на 60 литров, четырех алюминиевых батарей по 8 секций каждая и 90 метров трубы PN25 (20 x 3.4).

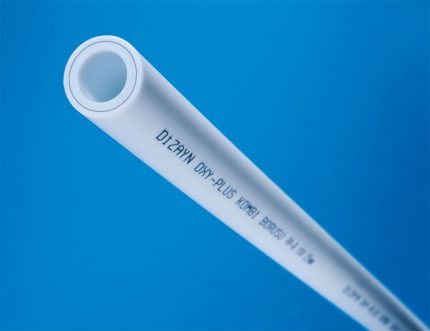
Трубы стандарта PN25 20 х 3.4 наиболее часто применяют для организации небольшого отопительного контура с последовательным подключением радиаторов. Ее внутренний диаметр равен 13.2 мм

Объем жидкости в трубе нужно посчитать в литрах. Для этого в качестве единицы измерения надо взять дециметр. Формулы перехода от стандартных величин длины следующие: 1 м = 10 дм и 1 мм = 0.01 дм.

Объем рубашки котла известен. V1 = 60 л.

В паспорте алюминиевого радиатора Elegance EL 500 указано, что объем одной секции равен 0.36 л. Тогда V2 = 4 * 8 * 0.36 = 11.5 л.

Вычислим суммарный объем труб. Их внутренний диаметр d = 20 – 2 * 3.4 = 13.2 мм = 0.132 дм. Длина l = 90 м = 900 дм. Следовательно:

V3 = π * l * d2 / 4 = 3.1415926 * 900 * 0.132 * 0.132 / 4 = 12.3 дм3 = 12.3 л.

Таким образом, теперь можно найти общий объем:

V = V1 + V2 + V3 = 60 + 11.5 + 12.3 = 83.8 л.

На промышленных и сельскохозяйственных объектах часто устанавливают самодельные радиаторы отопления, устроенные по типу регистров. Зная размеры труб, можно вычислить их объем

Расчет объема самодельного радиатора

Разберем, как рассчитать классический самодельный радиатор отопления из четырех горизонтальных труб длиной 2 м. Сначала необходимо найти площадь сечения. Измерить наружный диаметр можно с торца изделия.

Пусть он будет 114 мм. Используя таблицу стандартных параметров стальных труб, найдем толщину стенки, характерной для этого размера – 4.5 мм.

Вычислим внутренний диаметр:

d = 114 – 2 * 4.5 = 105 мм.

Определим площадь сечения:

S = π * d2 / 4 = 8659 мм2.

Суммарная длина всех фрагментов равна 8 м (8000 мм). Найдем объем:

V = l * S = 8000 * 8659 = 69272000 мм3.

Объем вертикальных соединительных трубок можно вычислить аналогичным образом. Но этой величиной можно и пренебречь, так как она будет составлять менее 0.1% от общего объема радиатора отопления.

Получившееся значение неинформативно, поэтому переведем его в литры. Так как 1 дм = 100 мм, то 1 дм3 = 100 * 100 * 100 = 1000000 = 106 мм3.

Поэтому V = 69272000 / 106 = 69.3 дм3 = 69.3 л.

Поэтому так как нужно будет посчитать объем труб в м3, то и все габариты перед подстановкой их в формулу надо будет сразу переводить в метры.

Дом в земле: фото

Как произвести расчет?

Рассчитываем сечение

Определение сечения трубы является несложной геометрической задачей. Для этого следует для начала воспользоваться формулой площади круга:

Sн= π Rн^2, (1)

где Rн – наружный радиус трубы, равен половине наружного диаметра.

Таким образом, мы определим площадь круга, образованного наружным диаметром.

Теперь определим площадь круга, образованного внутренним диаметром трубы. Для этого необходимо определить внутренний радиус, который определяется по следующей формуле:

Rвн=Rн-?, (2)

где? – толщина стенки трубы.

Определив площадь внутреннего круга Sве аналогично формуле (1), рассчитаем площадь сечения по формуле:

Sсеч=Sн?-S?вн.

Все действия можно свести в упрощенную формулу определения площади сечения:

Sсеч=? (?D_н/2?^2- ??/2?^2).

В качестве примера определим площадь сечения, внешний диаметр которого равен 1 метру, а толщина стенки – 10 мм.

Sсеч=3,14 (?1/2?^2- ?0,01/2?^2)=0,75 м^2.

Производим расчет площади внешней поверхности

Такой расчет также является геометрической задаче. Если развернуть трубу, то получится прямоугольник. Его ширина равна длине окружности внешней стенки трубы, а длина – длине.

Тогда площадь развертки трубы будет вычисляться по формуле:

S=? D_н L_тр,

где Lтр – длина трубы.

В качестве примера рассчитаем площадь поверхности под окраску теплотрассы, длина которой составляет 10 км, а внешний диаметр – 1 метр.

S=3,13 1 10000=31416 м^2.

Если говорить о количестве теплоизоляционного материала, то при подсчете следует учесть толщину слоя минеральной ваты.

Тогда формула примет вид:

S=? ?(D?_н+?2 ??_(в)) L_тр,

где?_в-толщина слоя минеральной ваты.

В действительности материала для теплоизоляции будет потрачено меньше, так как он накладывается в внахлест.

Производим расчет площади внутренней поверхности

Для начала необходимо определиться, для чего такой расчет следует проводить. Чаще всего он нужен при расчете гидродинамики движения теплоносителя в трубе. Внутренняя поверхность трубы является местом, где вода при её движении соприкасается с трубой. Таким образом, возникает гидравлическое сопротивление, которое необходимо учитывать при расчете сети коммуникации.

Необходимо помнить ряд следующих нюансов:

• При увеличении диаметра трубопровода снижается гидравлическое трение теплоносителя о стенки труб. Поэтому при большом диаметре и длине водопровода гидравлическое сопротивление трубы потоку воды можно не учитывать.
• Качество поверхности, её шероховатость, оказывает большое значение на величину гидравлического сопротивления. При этом такое влияние сильнее, чем зависимость сопротивления от площади поверхности внутренней стенки трубопровода. Так, полиэтиленовая труба обладает меньшей шероховатостью нежели ржавая металлическая. Поэтому величина гидравлического сопротивления в пластиковой трубе будет меньшей.
• Если в качестве материала для изготовления трубы применяется неоцинкованная сталь, то площадь поверхности внутренней стенки меняется во времени. На стенках такого трубопровода постепенно откладываются ржавчина и минеральные отложения. Как результат – происходит уменьшение внутреннего диаметра трубы и увеличение величины гидравлического сопротивления. Такой эффект необходимо учитывать при проектировании водопровода из стали.

S=? ?(D?_н-2 ?) L_тр.

В качестве примера рассчитаем трубу, диаметр которой равен одному метру, а толщина стенки – 10 мм.

S=3,14 (1-2 0,01) 10000=30788 м^2.

Заключение

Итак, приведенные в статье расчеты не являются сложными и доступны любому человеку. Они пригодятся при проектировании собственного трубопровода. Чтобы возведенная коммуникация соответствовала ожиданиям о её работоспособности, предложенные расчеты следует производить в обязательном порядке.

Сегодня нам предстоит небольшой экскурс в школьные программы геометрии и физики. Мы вспомним, как вычисляется площадь поперечного сечения трубы и ее внутренний объем. Кроме того, нам предстоит выяснить, как изменения диаметра трубопровода действуют на давление в потоке жидкости. Итак, в путь.

На фото — водогазопроводные трубы. Нам предстоит научиться вычислять их внутреннее сечение.

Какой кабель выбрать для квартирной проводки

Несмотря на дешевизну алюминиевых проводников, от их применения лучше отказаться. Причина – низкая надежность контактов, через которые будут проходить токи. Второй повод – несоответствие сечения провода мощности современной бытовой техники. Кабель из меди отличается надежностью, длительным сроком эксплуатации.

В квартирах и домах допускается использовать провод с маркировкой:

• ПУНП – плоский проводник с медными жилами в ПВХ-оболочке. Рассчитан на напряжение номиналом 250 В при частоте 50 Гц.
• ВВГ/ВВГнг – плоские кабели из меди с двойным ПВХ-покрытием. Применяются внутри и снаружи сооружений, не подвержены возгоранию. Бывают с 2-мя, 3-мя и 4-мя жилами.
• NYM – провод из меди для внутренней одиночной линии. Имеет изоляционную ПВХ-оболочку и наружное покрытие, жилы с заземлением и без него.

При выборе количества жил понадобится учесть способность токопроводимости на единицу сечения. В данном случае квартирную сеть лучше сделать из одножильного провода, толщина которого больше. Многожильные элементы можно изгибать многократно, подсоединять на них электроприборы. Качественным будет только кабель с тонкими жилами.

Физика явления [ править | править код ]

Высокая электропроводность металлов связана с тем, что в них имеется большое количество носителей тока — электронов проводимости

, образующихся из валентных электронов атомов металла, которые не принадлежат определённому атому. Электрический ток в металле возникает под действием внешнего электрического поля, которое вызывает упорядоченное движение электронов. Движущиеся под действием поля электроны рассеиваются на неоднородностях ионной решётки (на примесях, дефектах решётки, а также нарушениях периодической структуры, связанной с тепловыми колебаниями ионов). При этом электроны теряют импульс, а энергия их движения преобразуются во внутреннюю энергию кристаллической решётки, что и приводит к нагреванию проводника при прохождении по нему электрического тока.

Читать также: 12 Вольтовый регулятор оборотов

В других средах (полупроводниках, диэлектриках, электролитах, неполярных жидкостях, газах и т. д.) в зависимости от природы носителей заряда физическая причина сопротивления может быть иной. Линейная зависимость, выраженная законом Ома, соблюдается не во всех случаях.

Сопротивление проводника при прочих равных условиях зависит от его геометрии и от удельного электрического сопротивления

материала, из которого он состоит.

Сопротивление однородного проводника постоянного сечения зависит от свойств вещества проводника, его длины, сечения и вычисляется по формуле:

R = ρ ⋅ l S , < ho cdot l>>,>

где ρ — удельное сопротивление

вещества проводника, Ом·м,l — длина проводника, м, аS — площадь сечения, м².

Сопротивление однородного проводника также зависит от температуры.

Удельное сопротивление — скалярная физическая величина, численно равная сопротивлению однородного цилиндрического проводника единичной длины и единичной площади сечения.

Сопротивление металлов снижается при понижении температуры; при температурах порядка нескольких кельвинов сопротивление большинства металлов и сплавов стремится или становится равным нулю (эффект сверхпроводимости). Напротив, сопротивление полупроводников и изоляторов при снижении температуры (в некотором диапазоне) растёт. Сопротивление также меняется по мере увеличения тока/напряжения, протекающего через проводник/полупроводник.

Как вычислить площадь сечения

19.03.2018

Определение вспомогательных данных:

Внутренняя ширина

…идет расчет внутренней ширины полого прямоугольника… мм;

Внутренняя высота

…идет расчет внутренней высоты полого прямоугольника… мм.

Решение:

Площадь сечения

…идет расчет площади сечения полого прямоугольника… мм2;

Осевые моменты инерции относительно центральных осей

…идет расчет момента инерции полого прямоугольника относительно оси ОХ… мм4;

…идет расчет момента инерции полого прямоугольника относительно оси ОY… мм4;

Моменты сопротивления изгибу

…идет расчет момента сопротивления изгибу полого прямоугольника относительно оси ОХ… мм3;

…идет расчет момента сопротивления изгибу полого прямоугольника относительно оси ОY… мм3;

Радиусы инерции сечения

…идет расчет радиуса инерции полого прямоугольника относительно оси ОХ… мм;

…идет расчет радиуса инерции полого прямоугольника относительно оси ОY… мм.

Примечание: Использование данного онлайн калькулятора позволяет вычислить геометрические характеристики плоского сечения в виде полого прямоугольника (площадь, моменты инерции, моменты сопротивления изгибу, радиусы инерции) по известным линейным размерам. Блок исходных данных выделен желтым цветом, блок вспомогательных данных — синим, блок решения — зеленым.

Вы можете использовать сервис определения геометрических характеристик плоского сечения онлайн абсолютно бесплатно.

Порядок действий при расчете характеристик полого прямоугольного сечения:1. Для проведения расчета требуется ввести ширину сечения b, высоту сечения h и соответствующие толщины стенок Sh и Sb.

2.

По введенным данным программа автоматически вычисляет внутреннюю ширину сечения b1 и высоту сечения h1. 3.

Результаты расчета площади, моментов сопротивления изгибу, моментов и радиусов инерции полого прямоугольного сечения выводятся автоматически.

4. На рисунке справа приведены необходимые размеры элементов сечения.

Социальные кнопки для Joomla

Площадь треугольника, площадь прямоугольника, площадь трапеции, площадь квадрата, площадь круга, площадь полукруга и сектора, площадь параллелограмма.

Справочно: число пи

Пример 1

Прямоугольный поднос имеет длину 900 мм и ширину 350 мм. Определить его площадь в а) мм2, б) в см2, в) в м2

Решение:

а) Площадь =длина*ширина=900*350=315000 мм2

б) 1 см2=100 мм2, следовательно,

315000 мм2=315000/100=3150 см2

1 м2=10000 см2, следовательно,

3150 см2=3150/10000=0.315 м2

Пример 2

Определить площадь поперечного сечения балки, изображенной на рисунке.

Сечение балки можно разделить на три отдельных прямоугольника, как показано на рисунке

Sa=3*50=150 мм2

Sb=(65-5-3)*4=228 мм2

Sc=60*5=300 мм2

Общая площадь балки 150+228+300=678 мм2=6.78 см2.

Пример 3

Определить площадь дорожки, показанной на рисунке.

Решение:

Площадь дорожки = площадь большого прямоугольника — площадь малого прямоугольника

S=35*15-29*11=206 м2

Пример 4

Определить площадь параллелограмма, показанного на рисунке (размеры приведены в миллиметрах).

Тогда

202=(36-30)2+h2

h2=202-62=164

h=14,3 (приблизительно)

Следовательно, Sabcd=30*14.3=429 мм2

Пример 5

Показана боковая сторона здания. Определить площадь кирпичной кладки на боковой стороне.

Боковая сторона состоит из прямоугольника и треугольника.

Sпрям.=6*10=60 м2

S треуг. =1/2*основание*высота

CD=5 м, AD=6 м, следовательно, AC=3 м (по т. Пифагора). Следовательно,

S треуг. =1/2*10*3=15 м2.

Общая площадь кирпичной кладки есть 60+15=75 м2

Пример 6

S=πr2 или πd2/4.

а) S=πr2=π(3)2=9π=28.26 см2

б) S=πd2/4=π(10)2/4=100π/4=78.5 мм2

в) Длина окружности с=2πr, следовательно,

r=c/2π=60/2π=30/π

S=πr2=π(30/π)2=286.62 мм2

Пример 7

Вычислить площадь правильного восьмиугольника со стороной 5 см и поперечником 10 см.

Восьмиугольник — это многоугольник с 8 сторонами. Если из центра многоугольника провести лучи к вершинам, получится восемь одинаковых треугольников.

S треуг. =1/2*основание*высота=1/2*5*10/2=12.5 см2

Площадь восьмиугольника есть 8*12.5=100 см2

 Пример 8

Определить площадь правильного шестиугольника со стороной 10 см.

Другие два угла каждого треугольника составляют в сумме 120о и равны между собой.

Следовательно, все треугольники являются равносторонними с углами 60о и стороной 10 см

S треуг. =1/2*основание*высота

Высоту h находим по теореме Пифагора:

102=h2+52

Отсюда h2=100-25=75

h=8.66 см

Следовательно, S треуг. =1/2*10*8.66=43.3 см 2

Площадь шестиугольника равна 6*43.3=259.8 см2

Определение величины

Площадь — это величина, характеризующая размер геометрической фигуры. Её определение — одна из древнейших практических задач. Древние греки умели находить площадь многоугольников: так, каменщикам, чтобы узнать размер стены, приходилось умножать её длину на высоту.

По прошествии долгих лет трудом многих мыслителей был выработан математический аппарат для расчета этой величины практически для любой фигуры.

На Руси существовали особые единицы измерения: копна, соха, короб, верёвка, десятина, четь и другие, так или иначе связанные с пахотой. Две последних получили наибольшее распространение. Однако от древнерусских землемеров нам досталось только само слово — «площадь».

С развитием науки и техники появилось не только множество формул для расчёта площадей любых геометрических фигур, но и приборы, которые делают это за человека. Такие приборы называют планиметрами.

От слов к делу

Существует несколько способов замера диаметров трубы, отличающихся своими особенностями в зависимости от условий, которые важно учитывать для того, чтобы избежать ошибок. Выбор конкретного способа замера часто зависит от доступности к объекту замера

Рассмотрим некоторые из них.

Чаще всего для измерения диаметра трубы применяют общеизвестный штангенциркуль. Но его у вас может не быть или при его наличии большой диаметр трубы измерить с его помощью не представляется возможным. В этом случае применяется самый простой набор инструментов и знаний:

• гибкая линейка (по типу измерительной ленты, применяемой в швейном деле);
• рулетка;
• школьные знания числа Пи (оно равно 3,14).

Подобным набором средств можно измерять диаметр не только трубы, но и любого другого круглого объекта – прута, колонны или садовой клумбы.

Нам потребуется сделать лишь один замер – определить длину окружности трубы с помощью рулетки или гибкой линейки. Для этого сантиметровую ленту или рулетку накладывают на поверхность трубы в самой широкой ее части. Полученное значение окружности следует поделить на 3,14. Для более точных размеров применяют значение — 3,1416.

Следует заметить, что импортные поставки труб сопровождаются документацией, в которой уже указаны значения диаметров труб в дюймах. Для перевода этих значений в сантиметры их умножают на 2,54. Аналогично для обратного перевода сантиметров в дюймы – умножают на 0,398.

Измерения осуществляются с помощью штангенциркуля без каких-либо математических вычислений. Условие – полная доступность к трубе. Этот способ пригоден для измерения доступных труб небольшого диаметра (не более 15 см). Для осуществления замера ножки штангенциркуля прикладывают к торцу трубы и плотно их зажимают на внешних стенках. Полученное значение на шкале штангенциркуля с точностью до десятых частей миллиметра и будет наружным диаметром трубы.

Если торцевая часть трубы недоступна для осуществления замера, то есть, когда труба является смонтированным элементом уже действующей схемы водо- или газоснабжения, то для замеров штангенциркуль прикладывают к боковой поверхности трубы

В данном случае важное условие для осуществления обмера: длина ножек штангенциркуля должна превышать половину диаметра трубы

Видео

Видео